【题目】如图,![]() ,
,![]() 平分
平分![]() ,点
,点![]() 、
、![]() 在射线
在射线![]() 、
、![]() 上,点
上,点![]() 是射线
是射线![]() 上的一个动点,连接
上的一个动点,连接![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() .
.


(1)如图1,若DE//OB.
①![]() 的度数是________,当
的度数是________,当![]() 时,
时,![]() ________;
________;
②若![]() ,求
,求![]() 的值;
的值;
(2)如图2,若![]() ,是否存在这样的
,是否存在这样的![]() 的值,使得
的值,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
参考答案:
【答案】(1)①20°;70;②![]() ;(2)存在这样的
;(2)存在这样的![]() 的值,使得
的值,使得![]() .
.![]() 或104.
或104.
【解析】
(1)①先根据角平分线的定义求出∠BOC的度数,然后根据平行线的性质即可求出![]() 的度数;当
的度数;当![]() 时,在直角△ODF中根据三角形的内角和定理解答即可;
时,在直角△ODF中根据三角形的内角和定理解答即可;
②由于![]() 的度数已求出,且
的度数已求出,且![]() ,可先根据三角形的内角和求出
,可先根据三角形的内角和求出![]() 的度数,然后利用三角形的外角性质解答即可;
的度数,然后利用三角形的外角性质解答即可;
(2)先根据直角三角形两锐角互余的性质求出∠DEO的度数,然后分![]() 在
在![]() 左侧和
左侧和![]() 在
在![]() 右侧两种情况,分别画出符合题意的图形,然后利用三角形的内角和定理和三角形的外角性质解答即可.
右侧两种情况,分别画出符合题意的图形,然后利用三角形的内角和定理和三角形的外角性质解答即可.
解:(1)①![]() ,
,![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ;
;
故答案为:20°,70;
②![]() ,
,![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ;
;
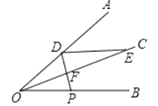
(2)存在这样的![]() 的值,使得
的值,使得![]() .
.
![]() ,
,![]() ,
,
在Rt![]() 中,
中,![]() .
.
①若![]() 在
在![]() 左侧,如图,
左侧,如图,
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;

②若![]() 在
在![]() 右侧,如图,
右侧,如图,
![]() 是
是![]() 的外角,
的外角,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
综上所述:![]() 或104.
或104.

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中,每个小正方形的边长为1个单位长度建立如图所示的平面直角坐标系,
 的顶点均为格点,把
的顶点均为格点,把 向左平移5个单位长度,再向下平移2个单位长度,得到
向左平移5个单位长度,再向下平移2个单位长度,得到 .
.
(1)在图中画出
 ;
;(2)点
 在
在 轴上,且
轴上,且 与
与 的面积相等,则点
的面积相等,则点 的坐标为 ;
的坐标为 ;(3)横、纵坐标均为整数的点称为整数点,在第一象限中的整数点
 满足
满足 ,直接写出整数点
,直接写出整数点 的所有可能坐标.
的所有可能坐标. -
科目: 来源: 题型:
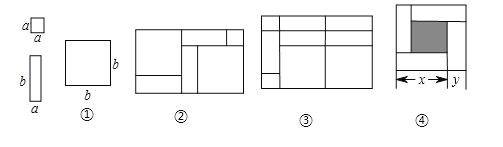
查看答案和解析>>【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式,比如图②可以解释为:
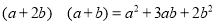
(1)图③可以解释为等式: .
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示
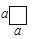 块,
块,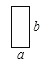 块,
块,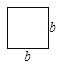 块.
块.(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个小长方形的两边长(x>y),观察图案,以下关系式正确的是 (填序号).
①
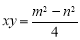 ,②
,② ,③
,③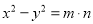 ,④
,④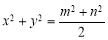
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线
 ,点
,点 ,
, 在直线
在直线 上,点
上,点 ,
, 在直线
在直线 上,且
上,且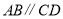 ,若
,若 保持不动,线段
保持不动,线段 向右匀速平移,如图2反映了
向右匀速平移,如图2反映了 的长度
的长度 随时间
随时间 的变化而变化的情况,则:
的变化而变化的情况,则:


(1)在线段
 开始平移之前,
开始平移之前,
 ;
;(2)线段
 向右平移了
向右平移了  ,向右平移的速度是
,向右平移的速度是  ;
;(3)如图3反映了
 的面积
的面积 随时间
随时间 的变化而变化的情况,则
的变化而变化的情况,则①平行线
 ,
, 之间的距离是
之间的距离是  ;
;②当
 时,直接写出
时,直接写出 关于
关于 的函数关系式(不必化简).
的函数关系式(不必化简). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1(注:与图2完全相同),二次函数y=
 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.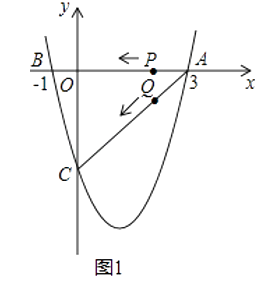
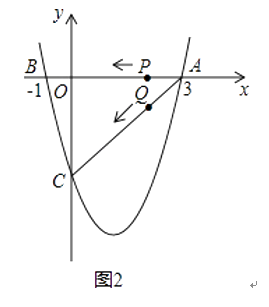
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索). -
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )
A.
B.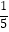
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,若有一动点
,若有一动点 从
从 出发,沿
出发,沿 匀速运动,则
匀速运动,则 的长度
的长度 与时间
与时间 之间的关系用图像表示大致是( )
之间的关系用图像表示大致是( )
A.
 B.
B.
C.
 D.
D.
相关试题

