【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式,比如图②可以解释为:![]()
(1)图③可以解释为等式: .
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示![]() 块,
块,![]() 块,
块,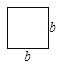 块.
块.
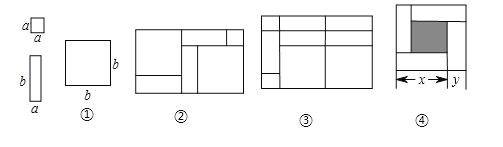
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个小长方形的两边长(x>y),观察图案,以下关系式正确的是 (填序号).
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]()
参考答案:
【答案】(1)![]() (2)2,7,3 (3)①②③④
(2)2,7,3 (3)①②③④
【解析】
(1)根据正方形和矩形的面积公式求解即可.
(2)将![]() 展开化简即可得出答案.
展开化简即可得出答案.
(3)逐项按照平方差公式及图形验证即可.
(1)图③可得,长为![]() ,宽为
,宽为![]() 的矩形的面积等于2个边长为
的矩形的面积等于2个边长为![]() 的正方形的面积加2个边长为
的正方形的面积加2个边长为![]() 的正方形的面积加5个长为
的正方形的面积加5个长为![]() ,宽为
,宽为![]() 的矩形的面积
的矩形的面积
故![]() .
.
(2)![]()
故答案为:2,7,3.
(3)∵![]()
∴![]() ,故①正确
,故①正确
∵![]()
∴②正确
∵![]()
∴![]() ,即
,即![]() ,故③正确
,故③正确
∵![]()
∴④正确
故答案为:①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地某一时刻的地面温度是26℃,每升高
 ,温度下降6℃,下面是温度(℃)与距离地面的高度
,温度下降6℃,下面是温度(℃)与距离地面的高度 对应的数值:
对应的数值:
0
1
2
3
4
5
…

26
20
14
8


…
根据上表,请完成下面的问题.
(1)表中
 ;
;(2)直接写出温度
 与高度
与高度 之间的函数关系式,并写出其中的常量和变量;
之间的函数关系式,并写出其中的常量和变量;(3)求该地距地面
 处的温度.
处的温度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中,每个小正方形的边长为1个单位长度建立如图所示的平面直角坐标系,
 的顶点均为格点,把
的顶点均为格点,把 向左平移5个单位长度,再向下平移2个单位长度,得到
向左平移5个单位长度,再向下平移2个单位长度,得到 .
.
(1)在图中画出
 ;
;(2)点
 在
在 轴上,且
轴上,且 与
与 的面积相等,则点
的面积相等,则点 的坐标为 ;
的坐标为 ;(3)横、纵坐标均为整数的点称为整数点,在第一象限中的整数点
 满足
满足 ,直接写出整数点
,直接写出整数点 的所有可能坐标.
的所有可能坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线
 ,点
,点 ,
, 在直线
在直线 上,点
上,点 ,
, 在直线
在直线 上,且
上,且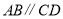 ,若
,若 保持不动,线段
保持不动,线段 向右匀速平移,如图2反映了
向右匀速平移,如图2反映了 的长度
的长度 随时间
随时间 的变化而变化的情况,则:
的变化而变化的情况,则:


(1)在线段
 开始平移之前,
开始平移之前,
 ;
;(2)线段
 向右平移了
向右平移了  ,向右平移的速度是
,向右平移的速度是  ;
;(3)如图3反映了
 的面积
的面积 随时间
随时间 的变化而变化的情况,则
的变化而变化的情况,则①平行线
 ,
, 之间的距离是
之间的距离是  ;
;②当
 时,直接写出
时,直接写出 关于
关于 的函数关系式(不必化简).
的函数关系式(不必化简). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
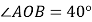 ,
, 平分
平分 ,点
,点 、
、 在射线
在射线 、
、 上,点
上,点 是射线
是射线 上的一个动点,连接
上的一个动点,连接 交射线
交射线 于点
于点 ,设
,设 .
.

(1)如图1,若DE//OB.
①
 的度数是________,当
的度数是________,当 时,
时, ________;
________;②若
 ,求
,求 的值;
的值;(2)如图2,若
 ,是否存在这样的
,是否存在这样的 的值,使得
的值,使得 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1(注:与图2完全相同),二次函数y=
 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.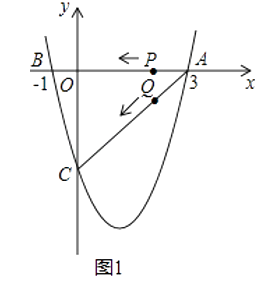
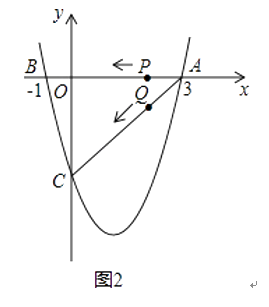
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
相关试题

