【题目】以下两个问题,任选其一作答.
如图,OD是∠AOC的平分线,OE是∠BOC的平分线.
问题一:若∠AOC=36°,∠BOC=136°,求∠DOE的度数.
问题二:若∠AOB=100°,求∠DOE的度数.

参考答案:
【答案】问题一:50°;问题二:50°.
【解析】试题分析:(1)利用角平分线的定义得出∠DOC=18°,∠EOC=68°进而求出∠DOE的度数;
(2)由角平分线得出∠DOE=![]() ∠AOB即可.
∠AOB即可.
试题解析:问题一:
∵OD平分∠AOC,∠AOC=36°,
∴∠DOC=![]() ∠AOC=18°.
∠AOC=18°.
∵OE平分∠BOC,∠BOC=136°,
∴∠EOC=![]() ∠BOC=68°.
∠BOC=68°.
∴∠DOE=∠EOC-∠DOC=50°.
问题二:
∵OD平分∠AOC,
∴∠DOC=![]() ∠AOC.
∠AOC.
∵OE平分∠BOC,
∴∠EOC=![]() ∠BOC.
∠BOC.
∴∠DOE=∠EOC-∠DOC=![]() ∠BOC
∠BOC![]() ∠AOC=
∠AOC=![]() ∠AOB.
∠AOB.
∵∠AOB=100°,
∴∠DOE=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,Rt△ABC中,∠ACB=90°,点D、E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(2)如图2,在△ABC中,∠ACB=40°,点D、E在直线AB上,且AD=AC,BE=BC,则∠DCE的度数;
(3)在△ABC中,∠ACB=n°(0<n<180°),点D、E在直线AB上,且AD=AC,BE=BC,求∠DCE的度数(直接写出答案,用含n的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究:如图①,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
请将下面的解答过程补充完整,并填空(理由或数学式)
解:∵DE∥BC,∴∠DEF= .( )
∵EF∥AB,∴ =∠ABC.( )
∴∠DEF=∠ABC.(等量代换)
∵∠ABC=40°,∴∠DEF= °.
(2)应用:如图②,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB的延长线上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=60°,则∠DEF= °.

-
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如: 等.那么如何求出它们的解集呢?
等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若a>0,b>0,则 >0;若a<0,b<0,则
>0;若a<0,b<0,则 >0;
>0;
(2)若a>0,b<0,则 <0;若a<0,b>0,则
<0;若a<0,b>0,则 <0.
<0.
反之:(1)若 >0,则
>0,则 或
或
(2) <0,则____________ .
<0,则____________ .
根据上述规律,求不等式 >0的解集.
>0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 与
与 轴、
轴、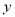 轴分别相交于点A,B,四边形ABCD是正方形,抛物线
轴分别相交于点A,B,四边形ABCD是正方形,抛物线 在经过A,D两点.
在经过A,D两点.
(1)求该抛物线表达式;
(2)连接BD,将线段BD绕着D点顺时针旋转90度,得到DB’.直接写出点B’的坐标,并判断点B’是否落在抛物线上,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示有一块直角三角形纸片,两直角边分别为:AC =6cm,BC = 8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )

A.2 cm
B.3 cm
C.4 cm
D.5 cm -
科目: 来源: 题型:
查看答案和解析>>【题目】一种商品每件成本a元,原来按成本增加25%定出价格,现在由于库存积压减价,按原价的90%出售,现售价多少元?每件还能盈利多少元?
相关试题

