搜索
【题目】如图所示有一块直角三角形纸片，两直角边分别为：AC =6cm，BC = 8 cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）
A.2 cm
B.3 cm
C.4 cm
D.5 cm
参考答案：
【答案】B
【解析】
先根据勾股定理求得AB的长，再根据折叠的性质求得AE，BE的长，从而利用勾股定理可求得CD的长．
∵AC=6cm，BC=8cm，∠C=90°
∴AB=10cm，
∵AE=6cm（折叠的性质)，
∴BE=4cm，
设CD=x，
则在Rt△DEB中，
42+x2=（8-x)2 ，
∴x=3cm．
故选：B．
【考点精析】本题主要考查了翻折变换（折叠问题）的相关知识点，需要掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】自学下面材料后，解答问题．
分母中含有未知数的不等式叫分式不等式．如：
等．那么如何求出它们的解集呢？
根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负．其字母表达式为：
（1）若a＞0，b＞0，则
＞0；若a＜0，b＜0，则＞0；
（2）若a＞0，b＜0，则＜0；若a＜0，b＞0，则＜0．
反之：（1）若＞0，则
或
（2）＜0，则____________ ．
根据上述规律，求不等式
＞0的解集． -
科目： 来源： 题型：
查看答案和解析>>【题目】以下两个问题，任选其一作答．
如图，OD是∠AOC的平分线，OE是∠BOC的平分线．
问题一：若∠AOC=36°，∠BOC=136°，求∠DOE的度数．
问题二：若∠AOB=100°，求∠DOE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线
与
轴、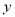
轴分别相交于点A，B，四边形ABCD是正方形，抛物线
在经过A，D两点.
（1）求该抛物线表达式；
（2）连接BD，将线段BD绕着D点顺时针旋转90度，得到DB’.直接写出点B’的坐标，并判断点B’是否落在抛物线上，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一种商品每件成本a元，原来按成本增加25%定出价格，现在由于库存积压减价，按原价的90%出售，现售价多少元？每件还能盈利多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图为一个平行四边形ABCD，其中H、G两点分别在BC、CD上，AH⊥BC，AG⊥CD，且AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4四个角．若AH=5，AG=6，则下列关系何者正确（ ）
A.∠1=∠2
B.∠3=∠4
C.BH=GD
D.HC=CG -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1,已知抛物线
与
轴交于A,B（点A在点B的右边），与
轴交于点C.过A,C两点作直线
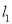，P是抛物线上的动点，过P作PD⊥
轴，垂足为D，交直线
于点E.设点P的横坐标为
.（1）求直线
的函数表达式;（2）问是否存在点P，使O,E,C,P四点能构成平行四边形,若存在，请求出
的值；若不存在，请说明理由.（3）如图2，过A点作直线
⊥
,连接OE,作△AOE的外接圆,交直线
于点F,连接OF,EF.当△EOF的面积最小时,求点P的坐标和最小值.
相关试题
