【题目】如图,根据图中信息解答下列问题:
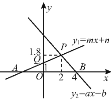
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
参考答案:
【答案】:(1) x<4;(2) x<0;(3)x≤2;(4)2<x<4.
【解析】
(1)求ax+b>0的解集,只需确定直线y2在x轴上方时x的取值范围即可;
(2)求mx+n<1的解集,也就是求直线y1在y=1下方时x的取值范围,据此解答即可;
(3)找出直线y1在直线y2的下方与相交时x的取值范围,据此可确定y1≤y2时x的取值范围;
(4)根据函数图象,找出直线y2在直线y1的下方且在x轴上方时x的取值范围即可.
(1)∵直线y2=ax+b与x轴的交点是(4,0),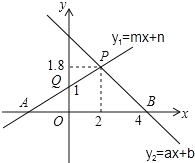
∴当x<4时, y2>0,即不等式ax+b>0的解集是x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时, y1<1,即不等式mx+n<1的解集是x<0;。
(3)由一次函数的图象知,两条直线的交点坐标是(2,1.8),当函数y1的图象在y2的下面时,有x2,
所以当x2时, y1 y2;
(4)如图所示,当2<x<4时,0< y2< y1.
故答案为:(1) x<4; (2) x<0; (3)x≤2; (4)2<x<4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.
(1)证明:RP=RQ;
(2)请探究下列变化:
A、变化一:交换题设与结论.已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.证明:RQ为⊙O的切线.

B、变化二:运动探求. ①如图2,若OA向上平移,变化一中结论还成立吗?(只交待判断) 答:_________.
②如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,原题中的结论还成立吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA.

(1)求△OAB的面积;
(2)若抛物线y=-x2-2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位长度,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加某网店的“翻牌抽奖”活动.如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.

(1)如果随机翻1张牌,求抽中20元奖品的概率;
(2)如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,求所获奖品总值不低于30元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).

(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M是第三象限内⊙C上一点,∠BMO=120°,则圆心C的坐标为( )

A. (1,1) B. (1,
 ) C. (2,1) D. (﹣
) C. (2,1) D. (﹣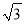 ,1)
,1)
相关试题

