Question

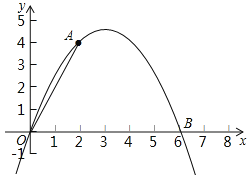
【题目】如图，二次函数y=ax2+bx的图象经过点A（2，4）与B（6，0）．

（1）求a，b的值；

（2）点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．

Answer 1

【答案】（1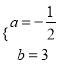）；（2）S关于x的函数表达式为S=﹣x2+8x（2＜x＜6），面积S有最大值为16．

【解析】试题分析：（1）把A与B坐标代入二次函数解析式求出a与b的值即可；
（2）如图，过A作x轴的垂直，垂足为D（2，0），连接CD，过C作CE⊥AD，CF⊥x轴，垂足分别为E，F，分别表示出三角形OAD，三角形ACD，以及三角形BCD的面积，之和即为S，确定出S关于x的函数解析式，并求出x的范围，利用二次函数性质即可确定出S的最大值，以及此时x的值．

试题解析：

(1)将点A(2，4)，B(6，0)的坐标分别代入y＝ax2＋bx，

得解得

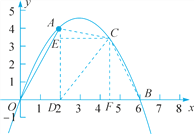
(2)如解图，过点A作x轴的垂线，垂足为D(2，0)，过点C作CE⊥AD，CF⊥x轴，垂足分别为E，F，连结AC，BC，CD.

则S△OAD＝OD·AD＝×2×4＝4，

S△ACD＝AD·CE＝×4×(x－2)＝2x－4，

S△BCD＝BD·CF＝×(6－2)×＝－x2＋6x，

∴S＝S△OAD＋S△ACD＋S△BCD＝4＋2x－4－x2＋6x＝－x2＋8x，

∴S关于x的函数表达式为S＝－x2＋8x(2＜x＜6)．

∵S＝－x2＋8x＝－(x－4)2＋16，

∴当x＝4时，四边形OACB的面积S有最大值，最大值为16.