【题目】已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
参考答案:
【答案】(1). a=-1 ![]() (2). P1(
(2). P1(![]() ,
,![]() ),P2(-
),P2(-![]() ,-
,-![]() ).
).
【解析】试题分析:(1)由于抛物线的图象经过点(-1,0),那么此点坐标必满足抛物线的解析式,将其代入抛物线的解析式中,即可求得a的值,进而可得到抛物线的顶点坐标.
(2)将点P(t,t)代入抛物线的解析式中,即可求得符合条件的不动点的坐标.
试题解析:
(1)把点(-1,0)的坐标代入y=ax2+x+2中,得a=-1.
∴此抛物线的函数表达式为y=-x2+x+2=-![]()
![]() +
+![]() ,其顶点坐标是
,其顶点坐标是![]() .
.
(2)把点P(t,t)的坐标代入y=-x2+x+2中,
得t=-t2+t+2,解得t1=![]() ,t2=-
,t2=-![]() .
.
∴此抛物线上的不动点有两个,即点P1(![]() ,
,![]() ),P2(-
),P2(-![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
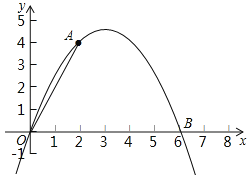
查看答案和解析>>【题目】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为4的正方形OABC置于平面直角坐标系中,点P在边OA上从O向A运动,连接CP交对角线OB于点Q,连接AQ.

(1)求证:△OCQ≌△OAQ;
(2)当点Q的坐标为( ,
,  )时,求点P的坐标;
)时,求点P的坐标;
(3)若点P在边OA上从点O运动到点A后,再继续在边AB上从A运动到点B,在整个过运动过程中,若△OCQ恰为等腰三角形,请直接写出所有满足条件的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列说法:
(1)无理数就是开方开不尽的数;
(2)无理数是无限不循环小数;
(3)无理数包括正无理数、零、负无理数;
(4)无理数都可以用数轴上的点来表示.
其中正确说法的个数是( )
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数关系中,不能看做二次函数y=ax2+bx+c(a≠0)模型的是( )
A. 圆的半径和其面积的变化关系
B. 我国人口年自然增长率x,两年中从12亿增加到y亿的x与y的变化关系
C. 掷铅球水平距离与高度的关系
D. 面积一定的三角形底边与高的关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知图1将线段AB向右平移1个单位长度,图2是将线段AB折一下再向右平移1个单位长度,请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形;

(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积;
(3)如图4,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求这块菜地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业的年收入约为700000元,数据“700000”用科学记数法可表示为( )
A.0.7×106
B.7×105
C.7×104
D.70×104
相关试题

