【题目】如图所示,在△ABC中,AD⊥BC于D,DE∥AC于E,DF∥AB交AC于F,连接EF。
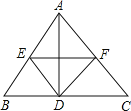
(1)当△ABC满足什么条件时,四边形AEDF是矩形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形,并说明理由。
参考答案:
【答案】(1)∠BAC=90°,理由见解析;(2)∠BAC=90°,且AB=AC,理由见解析
【解析】
试题(1)先由已知条件证出四边形![]() 是平行四边形,再由
是平行四边形,再由![]() 即可得出四边形
即可得出四边形![]() 是矩形;
是矩形;
(2)由(1)得:当![]() 时,四边形
时,四边形![]() 是矩形,再证出
是矩形,再证出![]() 即可得出四边形
即可得出四边形![]() 是正方形.
是正方形.
试题解析:(1)当△ABC满足∠BAC=90时,四边形AEDF是矩形;理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
又![]()
∴四边形AEDF是矩形;
(2)当△ABC满足![]() ,且AB=AC时,四边形AEDF是正方形;理由如下:
,且AB=AC时,四边形AEDF是正方形;理由如下:
由(1)得:当![]() 时,四边形AEDF是矩形,
时,四边形AEDF是矩形,
又∵AB=AC,
![]()
∵AD⊥BC,
∴△ABD和△ACD是等腰直角三角形,
∵DE∥AC,
∴DE⊥AB,
∴AE=BE,
![]() 同理:
同理:![]()
∴DE=DF,
∴四边形AEDF是正方形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|
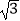 ﹣1|﹣
﹣1|﹣ 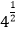 ﹣
﹣ 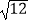 +
+ 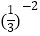 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求:
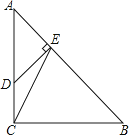
(1)线段BE的长;
(2)∠ECB的余切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题:
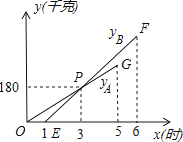
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人比A种机器人多搬运了多少千克? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,⊙O是△ABC的外接圆,
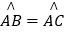 ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.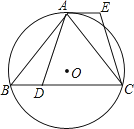
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣5(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.

(1)求这条抛物线的表达式;
(2)联结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
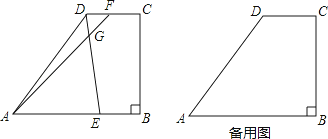
(1)求线段CD的长;
(2)如果△AEC是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.
相关试题

