【题目】某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题: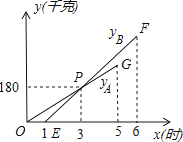
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人比A种机器人多搬运了多少千克?
参考答案:
【答案】
(1)
解:设yB关于x的函数解析式为yB=kx+b(k≠0).
将点(1,0)、(3,180)代入得: ![]() ,
,
解得:k=90,b=﹣90.
所以yB关于x的函数解析式为yB=90x﹣90(1≤x≤6)
(2)
解:设yA关于x的解析式为yA=k1x.
根据题意得:3k1=180.
解得:k1=60.
所以yA=60x.
当x=5时,yA=60×5=300(千克);
x=6时,yB=90×6﹣90=450(千克).
450﹣300=150(千克).
答:若果A、B两种机器人各连续搬运5小时,B种机器人比A种机器人多搬运了150千克
【解析】(1)设yB关于x的函数解析式为yB=kx+b(k≠0),将点(1,0)、(3,180)代入一次函数函数的解析式得到关于k,b的方程组,从而可求得函数的解析式;
(2)设yA关于x的解析式为yA=k1x.将(3,180)代入可求得yA关于x的解析式,然后将x=6,x=5代入一次函数和正比例函数的解析式求得yA , yB的值,最后求得yA与yB的差即可. 本题主要考查的是一次函数的应用,依据待定系数法求得一次函数的解析式是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了正方形之后,给同桌小文出了错题,从下列四个条件:
①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图所示),现有如下四种选法,你认为其中错误的是( )
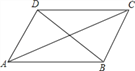
A. ①② B. ①③ C. ②③ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|
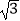 ﹣1|﹣
﹣1|﹣ 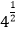 ﹣
﹣ 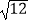 +
+ 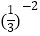 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,联结CE,求:
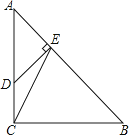
(1)线段BE的长;
(2)∠ECB的余切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AD⊥BC于D,DE∥AC于E,DF∥AB交AC于F,连接EF。
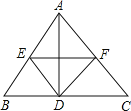
(1)当△ABC满足什么条件时,四边形AEDF是矩形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,⊙O是△ABC的外接圆,
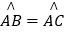 ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.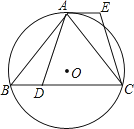
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣5(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.

(1)求这条抛物线的表达式;
(2)联结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标.
相关试题

