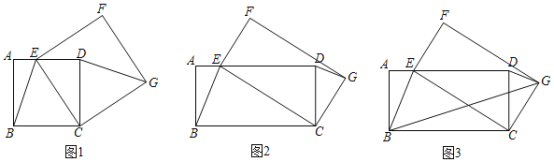
【题目】(问题情境)(1)如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是 ;
(类比探究)
(2)如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;
(拓展提升)
(3)如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为 .
参考答案:
【答案】(1)DG=BE;(2)![]() ,DG⊥BE;(3)4
,DG⊥BE;(3)4![]() .
.
【解析】
(1)通过证明△DCG和△BCE(SAS)全等,得到DG=BE.
(2)通过证明△DCG∽△BCE得到![]() ,所以
,所以![]() .∠BEC=∠DGC.延长BE、GD相交于点H.因为矩形ECGF,所以∠FEC=∠FGC=90°,所以∠HEF
.∠BEC=∠DGC.延长BE、GD相交于点H.因为矩形ECGF,所以∠FEC=∠FGC=90°,所以∠HEF
+∠BEC=180°-∠FEC=90°,∠FGH+∠DGC=90°,所以∠H=∠F=90°,所以DG⊥BE.
(3)作EN⊥BC于N,GM⊥BC交BC的延长线于M.首先证明点G的运动轨迹是线段GM,将2BG+BE的最小值转化为求2(BG+DG)的最小值.
(1)DG=BE
理由:
∵正方形ABCD,
∴CD=CB,∠BCD=90°
∵正方形ECGF,
∴CG=CE,∠ECG=90°
∴∠ECG=∠BCD=90°
∴∠DCG=∠BCE
在△DCG和△BCE中
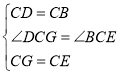
∴△DCG≌△BCE(SAS)
∴DG=BE
(2)![]() ,DG⊥BE.
,DG⊥BE.
理由如下:延长BE、GD相交于点H.
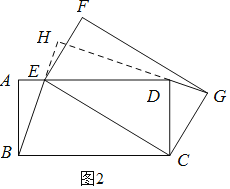
∵矩形ECGF、矩形ABCD,
∴∠ECG=∠BCD=90°,
∴∠DCG=∠BCE,
∵CD:CB=2:4=1:2,CG:CE=1:2,
∴CD:CB=CG:CE,
∵∠DCG=∠BCE,
∴△DCG∽△BCE,
∴![]() ,∠BEC=∠DGC,
,∠BEC=∠DGC,
∴![]()
∵矩形ECGF
∴∠FEC=∠FGC=∠F=90°
∴∠HEF+∠BEC=180°-∠FEC=90°,∠FGH+∠DGC=90°,
∴∠H=∠F=90°
∴DG⊥BE
(3)作EN⊥BC于N,GM⊥BC交BC的延长线于M.

易证△ECN∽△CGM,
∴![]() ,
,
∵EN=AB=2,
∴CM=1,
∴点G的运动轨迹是直线MG,
作点D关于直线GM的对称点G′,连接BG′交GM于G,此时BG+GD的值最小,最小值=BG′
由(2)知,![]()
∴BE=2DG
∴2BG+BE=2BG+2DG=2(BG+DG)
∴2BG+BE的最小值就是2(BG+DG)的最小值.
∵BG′=![]() ,
,
∴2BG+BE的最小值为4![]()
故答案为4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD,AB=6,BC=10,以BC所在直线为x轴,AB所在直线为y轴,建立如图所示的平面直角坐标系,在CD边上取一点E,将△ADE沿AE翻折,点D恰好落在BC边上的点F处.
(1)求线段EF长;
(2)在平面内找一点G,
①使得以A、B、F、G为顶点的四边形是平行四边形,请直接写出点G的坐标;
②如图2,将图1翻折后的矩形沿y轴正半轴向上平移m个单位,若四边形AOGF为菱形,请求出m的值并写出点G的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】 观察下列等式:
第1个等式:a1=
 =
= ×(
×( ﹣
﹣ );
);第2个等式:a2=
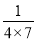 =
= ×(
×( ﹣
﹣ );
);第3个等式:a3=
 =
= ×(
×( ﹣
﹣ );
);第4个等式:a4=
 =
= ×(
×( ﹣
﹣ );
);…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
第n(n为正整数)个等式:an= = ;
(2)求a1+a2+a3+a4+…+a2019的值;
(3)数学符号
 =f(1)+f(2)+f(3)+…+f(n),试求
=f(1)+f(2)+f(3)+…+f(n),试求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇准备完成题目:化简:
 ,发现系数“
,发现系数“ ”印刷不清楚.
”印刷不清楚.(1)他把“
 ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
 ”是几?
”是几? -
科目: 来源: 题型:
查看答案和解析>>【题目】
 ABCD的两条对角线AC,BD交于点O,点E是CD的中点,△DOE的面积为l0cm2,则△ABD的面积为( )
ABCD的两条对角线AC,BD交于点O,点E是CD的中点,△DOE的面积为l0cm2,则△ABD的面积为( )
A.15cm2B.20cm2C.30cm2D.40cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个.

A.3B.4C.5D.6
相关试题

