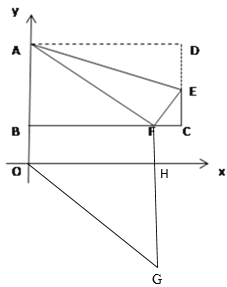
【题目】已知矩形ABCD,AB=6,BC=10,以BC所在直线为x轴,AB所在直线为y轴,建立如图所示的平面直角坐标系,在CD边上取一点E,将△ADE沿AE翻折,点D恰好落在BC边上的点F处.
(1)求线段EF长;
(2)在平面内找一点G,
①使得以A、B、F、G为顶点的四边形是平行四边形,请直接写出点G的坐标;
②如图2,将图1翻折后的矩形沿y轴正半轴向上平移m个单位,若四边形AOGF为菱形,请求出m的值并写出点G的坐标.

参考答案:
【答案】(1)EF=![]() ;(2)①点G的坐标为(-8,6)或(8,6)或(8,-6);②m=4,点G的坐标是(8,-6).
;(2)①点G的坐标为(-8,6)或(8,6)或(8,-6);②m=4,点G的坐标是(8,-6).
【解析】
(1)由矩形的性质得到AD=BC=10,CD=AB=6,由折叠得AF=AD=10,根据勾股定理求出OF=8,得到FC=OC-OF=2,再利用勾股定理得到![]() ,即可求出EF;
,即可求出EF;
(2)①分别以AB、AF、BF为平行四边形的对角线,根据平行四边形的性质得到点G的坐标;
②根据菱形的性质求出AO=AF=10,由此得到平移的距离m=4, 设FG交x轴于点H,证明四边形OBFH是矩形,得到=OB=4,OH=BF=8,求出HG=10-4=6,由此求出点G的坐标是(8,-6).
(1)∵四边形ABCD是矩形,
∴AD=BC=10,CD=AB=6,
由折叠得AF=AD=10,
∵∠AOC=90°,AO=6,
∴OF=8,
∴FC=OC-OF=2,
在Rt△EFC中,![]() ,
,
∴![]() ,
,
解得EF=![]() ;
;
(2)①当AB为平行四边形的对角线时,AG=BF且AG∥BF,∴点G的坐标为(-8,6);
当AF为平行四边形的对角线时,AG=BF且AG∥BF,∴点G的坐标为(8,6);
当BF为平行四边形的对角线时,FG=AB且FG∥AB,∴点G的坐标为(8,-6);
综上,点G的坐标为(-8,6)或(8,6)或(8,-6);
②∵四边形AOGF是菱形,
∴AO=AF=10,
∴矩形ABCD平移的距离m=AO-AB=10-6=4,即OB=4,
设FG交x轴于点H,
∵AO∥FG,BC∥x轴,
∴∠FBO=∠BOH=∠OHF=90°,
∴四边形OBFH是矩形,
∴FH=OB=4,OH=BF=8,
∴HG=10-4=6,
∴点G的坐标是(8,-6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E, DF∥AB交BC于点F .
(1)求证:四边形BEDF是菱形
(2)如果∠A=80°,∠C=30°,求∠BDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?

-
科目: 来源: 题型:
查看答案和解析>>【题目】 观察下列等式:
第1个等式:a1=
 =
= ×(
×( ﹣
﹣ );
);第2个等式:a2=
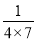 =
= ×(
×( ﹣
﹣ );
);第3个等式:a3=
 =
= ×(
×( ﹣
﹣ );
);第4个等式:a4=
 =
= ×(
×( ﹣
﹣ );
);…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
第n(n为正整数)个等式:an= = ;
(2)求a1+a2+a3+a4+…+a2019的值;
(3)数学符号
 =f(1)+f(2)+f(3)+…+f(n),试求
=f(1)+f(2)+f(3)+…+f(n),试求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇准备完成题目:化简:
 ,发现系数“
,发现系数“ ”印刷不清楚.
”印刷不清楚.(1)他把“
 ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
 ”是几?
”是几? -
科目: 来源: 题型:
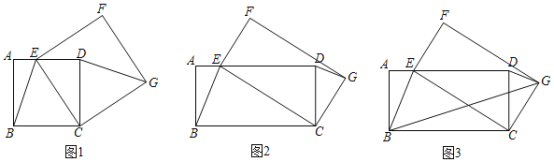
查看答案和解析>>【题目】(问题情境)(1)如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是 ;
(类比探究)
(2)如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;
(拓展提升)
(3)如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为 .
相关试题

