【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.
(1)求每个小矩形的长与宽;
(2)在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1 , E2…表示)
(3)求sin∠ACB的值.
参考答案:
【答案】
(1)
解:设每个小矩形的长为x,宽为y,
依题意得: ![]() ,
,
解得 ![]() ,
,
所以每个小矩形的长为2,宽为1
(2)
解:如图所示:

(3)
解:由图可知,S△ABC=4,设AC边上的高线为h,可知, ![]() ACh=4.
ACh=4.
∵由图可计算AC=2 ![]() ,BC=
,BC= ![]() ,
,
∴h= ![]() ,
,
∴sin∠ACB= ![]() =
= ![]() =
= ![]()
【解析】(1)设每个小矩形的长为x,宽为y,根据图形可知小矩形的长与宽间的数量关系有两个:2个矩形的宽=矩形的长;两个矩形的宽+1个矩形的长=4,据此列出方程组,并解答即可;(2)利用图形和勾股定理逆定理进行解答;(3)利用面积法求得边AC上的高,然后由锐角三角函数的定义进行解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.

(1)求证:△BDE≌△ADC;
(2)若BC=8.4,tanC= ,求DE的长.
,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的内切圆,切点为D,E,F,若AD、BE的长为方程
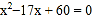 的两个根,则△ABC的周长为 ______.
的两个根,则△ABC的周长为 ______.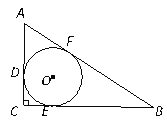
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l与x轴,y轴分别交于M,N两点,且OM=ON=3.
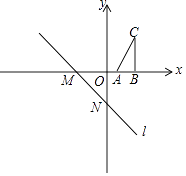
(1)求这条直线的函数表达式;
(2)Rt△ABC与直线l在同一个平面直角坐标系内,其中∠ABC=90°,AC=2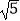 ,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积.
,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径为4,OA为半径,CD为弦,OA与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线.
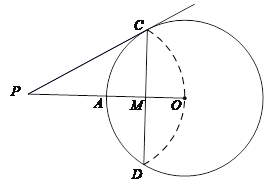
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,第一学习小组合作探究后,得到DE﹣BF=EF,请证明这个结论;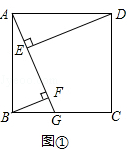
(2)若(1)中的点G在CB的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时BF,DE,EF之间的数量关系;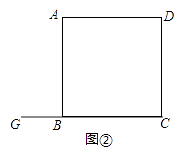
(3)如图③,四边形ABCD内接于⊙O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由.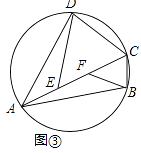
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体的六个面上分别标有1、2、3、4、5、6,根据图中从各个方向看到的数字,解答下面的问题:“?”处的数字是_____.

相关试题

