【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD,DE∥AC.
(1)求证:四边形 OCED 为菱形
(2)若AD=7,AB=4,求四边形 OCED的面积.

参考答案:
【答案】(1)证明见解析;(2)S菱形OCED=14
【解析】分析:(1)根据已知条件CE∥BD,DE∥AC即可得四边形DOCE是平行四边形,再利用矩形的性质得出DO=CO,根据一组邻边相等的平行四边形为矩形即可证得结论;(2)连接OE,证明四边形AOED是平行四边形,根据平行四边形的性质求得OE和CD的长,再利用菱形的面积公式即可求得四边形 OCED的面积.
详解:
(1)∵DE∥OC,CE∥OD,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴ AC=BD.
∴OC=OD,
∴平行四边形OCED是菱形.
(2)如图,连接OE,
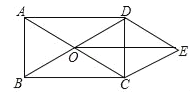
∵在菱形OCED中,OE⊥CD,
又∵AD⊥CD,∴OE∥AD,
∵DE∥AC,OE∥AD,
∴四边形AOED是平行四边形,
∴OE=AD=7,
∴S菱形OCED=![]() OEDC=
OEDC=![]() ×4×7=14.
×4×7=14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面一列数,探求其规律:
 ,-
,- ,
, ,-
,-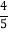 ,
, ,-
,- ,…
,…(1) 写出第7,8,9项的三个数;
(2) 第2 018个数是什么?
(3) 如果这一列数无限排列下去,与 ____ 、____ 两数越来越接近?
-
科目: 来源: 题型:
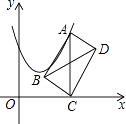
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中解为x=3的方程是( )
A. 3x+1=5x-5 B. 2(x+3)=-x+9
C. 3(1-2x)-2(x+3)=0 D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】老师在黑板上出了一道解方程的题:
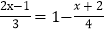 ,小明马上举起了手,要求到黑板上去做,他是这样做的:
,小明马上举起了手,要求到黑板上去做,他是这样做的:去分母,得4(2x-1)=1-3(x+2). ①
去括号,得8x-4=1-3x-6. ②
移项,得8x+3x=l-6+4 . ③
合并同类项,得11x=-1. ④
系数化为1,得x=-
 . ⑤
. ⑤老师说:小明解一元一次方程的一般步骤都掌握了,但解题时有一步做错了,他错在第 步(填编号),请你将正确的解方程过程写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣
 ,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号).
,y2)在该图象上,则y1>y2 . 其中正确的结论是(填入正确结论的序号). 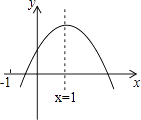
相关试题

