【题目】某核桃种植基地计划种植A、B两种优质核桃共30亩,已知这两种核桃的年产量分别为800千克/亩、1000千克/亩,收购价格分别是4.2元/千克、4元/千克.
(1)若该基地收获两种核桃的年总产量为25800千克,则A、B两种核桃各种植了多少亩?
(2)设该基地种植A种核桃a亩,全部收购后,总收入为w元,求出w与a之间的函数关系式.若要求种植A种核桃的面积不少于B种核桃的一半,那么种植A、B两种核桃各多少亩时,该种植基地的总收入最多?最多是多少元?
参考答案:
【答案】(1)A、B两种核桃各种植了21亩和9亩.(2)种植A、B两种核桃各10亩、20亩时,该种植基地的总收入最多,最多是113600元.
【解析】试题分析:(1)设该基地种植A种水果x亩,种植B种水果(30-x)亩,根据总产量的等量关系,可得一元一次方程,解一元一次方程即可解答;
(2)设该基地种植A种水果a亩,种植B种水果(30-a)亩,根据种植面积的关系可得a≥![]() (30-a),求解可得a的取值范围,根据题意得到w和a的关系式,利用一次函数的性质即可解答.
(30-a),求解可得a的取值范围,根据题意得到w和a的关系式,利用一次函数的性质即可解答.
解:(1)设A种核桃种植了x亩,由题意可得800x+1000(30-x)=25800,解得x=21,∴30-x=9.即A、B两种核桃各种植了21亩和9亩.
(2)由题意可得w=800a×4.2+1000(30-a)×4=120000-640a,即w与a之间的函数关系式为w=120000-640a.∵a≥![]() (30-a),∴a≥10,∴当a=10时,w=120000-640a取得最大值,此时w=113600,30-a=20,即种植A、B两种核桃各10亩、20亩时,该种植基地的总收入最多,最多是113600元.
(30-a),∴a≥10,∴当a=10时,w=120000-640a取得最大值,此时w=113600,30-a=20,即种植A、B两种核桃各10亩、20亩时,该种植基地的总收入最多,最多是113600元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周日上午小明从家跑步去图书馆,在那里看了一会儿书后又走到文具店去买笔记本,然后散步回家.下图反映的是小明离家的距离
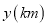 与所用时间
与所用时间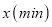 之间的函数关系,据此回答问题:
之间的函数关系,据此回答问题: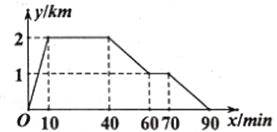
(1)图书馆离小明家
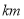 ,小明从家到图书馆用了
,小明从家到图书馆用了 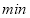 .
.(2)图书馆离文具店____
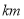 .
.(3)小明在文具店停留了
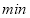
(4)小明从文具店回到家的平均速度是多少千米/小时?(写出简要计算过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是 ;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从
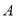 地向
地向 地打长途电话,按时收费,3分钟内收费2.7元,3分钟后,每通话1分钟收费1.2元.某人在
地打长途电话,按时收费,3分钟内收费2.7元,3分钟后,每通话1分钟收费1.2元.某人在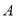 地向
地向 地打电话共用了
地打电话共用了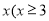 ,且
,且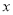 为整数)分钟,话费为
为整数)分钟,话费为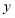 元.
元.(1)写出
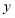 与
与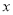 之间的函数关系式.
之间的函数关系式.(2)若通话5分钟,则需要话费多少元?
(3)若某次通话费用为8.7元,则他通话多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22019,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22019+22020
将下式减去上式得2S-S=22020-1
即S=22020-1
即1+2+22+23+24+…=22020-1
请你仿照此法计算:
(1)1+2+22+23+24+…+220
(2)1+5+52+53+54+…+5n(其中n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在探究一次函数
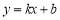 的图像性质时我们有如下发现:
的图像性质时我们有如下发现:①系数
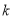 决定了函数图像的坡度,
决定了函数图像的坡度,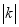 越大则图像坡度越大(越靠近
越大则图像坡度越大(越靠近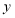 轴),
轴),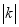 越小则图像坡度越小(越靠近
越小则图像坡度越小(越靠近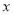 轴);
轴);②常数项
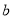 决定了图像与
决定了图像与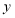 轴的交点,即函数图像与
轴的交点,即函数图像与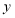 轴交点坐标始终为
轴交点坐标始终为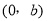 .
.基于以上发现,我们得出结论:如果两个一次函数的
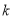 值相同,那么两个一次函数的图像平行.反之,如果两直线平行,则两条直线所对应的函数表达式的
值相同,那么两个一次函数的图像平行.反之,如果两直线平行,则两条直线所对应的函数表达式的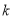 值一定相等:把函数图像沿
值一定相等:把函数图像沿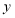 轴向上(或向下) 平移
轴向上(或向下) 平移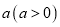 个单位, 系数
个单位, 系数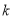 保持不变, 常数
保持不变, 常数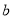 变为
变为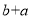 (或
(或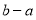 ).如:函数
).如:函数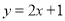 和
和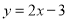 的图像互相平行:函数
的图像互相平行:函数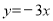 的图像向上平移2个单位后所得函数表达式为
的图像向上平移2个单位后所得函数表达式为 .
.据此回答下列问题:
(1) 把函数
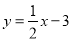 的图像向上平移4个单位后所得函数的表达式为____;
的图像向上平移4个单位后所得函数的表达式为____;(2)把函数
 的图像向 (上或下)平移 个单位可得到函数
的图像向 (上或下)平移 个单位可得到函数 的图像;
的图像;(3)若直线
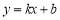 经过点
经过点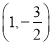 且与直线
且与直线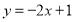 平行,求出直线
平行,求出直线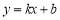 的表达式.
的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并回答问题.我们知道|a|的几何意义是指数轴上表示数的点与原点的距离,那么|a-b|的几何意义又是什么呢?我们不妨考虑一下,取特殊值时的情况.比如考虑|5-(-6)|的几何意义,在数轴上分别标出表示-6和5的点,(如图所示),两点间的距离是11,而|5-(-6)|=11,因此不难看出|5-(-6)|就是数轴上表示-6和5两点间的距离.
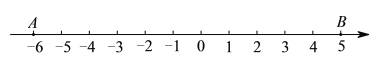
(1)|a-b|的几何意义是_______;
(2)当|x-2|=2时,求出x的值.
(3)设Q=|x+6|-|x-5|,请问Q是否存在最大值,若没有请说明理由,若有,请求出最大值.
相关试题

