【题目】在钝角三角形ABC中,把AB=AC,D是BC上一点,AD把![]() ABC分成两个等腰三角形,则
ABC分成两个等腰三角形,则![]() BAC的度数为( )
BAC的度数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
根据等腰三角形的性质可得∠B=∠BAD,∠ADC=∠DAC,∠B=∠C,再由三角形外角的性质可得∠ADC=∠B+∠BAD=2∠B,设∠B=x°,则∠DAC=∠ADC=2x°,∠BAC=3x°,由三角形的内角和定理可得x+x+3x=180,解方程求得x的值,即可求得![]() BAC的度数.
BAC的度数.
如图,
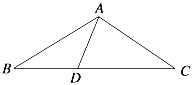
根据题意,△ABD、△ADC是等腰三角形,
∴∠B=∠BAD,∠ADC=∠DAC,
∵AB=AC,
∴∠B=∠C,
根据三角形外角的性质可得,
∠ADC=∠B+∠BAD=2∠B,
设∠B=x°,则∠DAC=∠ADC=2x°,∠BAC=3x°,
根据三角形内角和,x+x+3x=180,
解得x=36,
∴∠BAC=3x°=108°.
故选D.
-
科目: 来源: 题型:
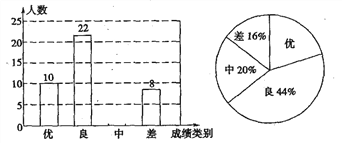
查看答案和解析>>【题目】为迎接2018年中考,我校对九年级学生进行了一次数学模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如图所示的两幅不完整的统计图,请你根据统计图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)求样本中表示成绩类别为“中”的人数,并将条形统计图补充完整;
(3)我校九年级共有700人参加了这次数学考试,请估计我校九年级共有多少名学生的数学成绩可以达到优秀?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“邮扬新干线”是指从高邮站开往扬州站的公交车,中途只停靠江都站,现甲、乙、丙3名不相识的乘客同时从高邮站上车。
(1)求甲、乙、丙三名乘客在同一个站下车的概率;
(2)求甲、乙、丙三名乘客中至少有一人在江都站下车的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的
 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:将连续的偶数2,4,6,8,…,排列如下表:
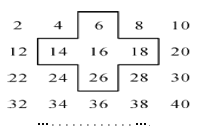
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)若将十字框上下左右移动,可框住另外的五个数,其他五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
-
科目: 来源: 题型:
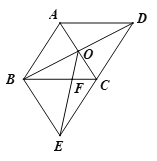
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,∠ABC=60°,过点B作AC的平行线交DC的延长线于点E.
(1) 求证:四边形ABEC为菱形;
(2) 若AB=6,连接OE,求OE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ ACB=115O,BD=BC,AE=AC. 则∠ECD的度数为_________.
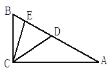
相关试题

