【题目】已知∠ACB=90°,AC=2,CB=4.点P为线段CB上一动点,连接AP,△APC与△APC′关于直线AP对称,其中点C的对称点为点C′.直线m过点A且平行于CB
(1)如图①:连接AB,当点C落在线段AB上时,求BC′的长;
(2)如图②:当PC=![]() BC时,延长PC′交直线m于点D,求△ADC′面积;
BC时,延长PC′交直线m于点D,求△ADC′面积;
(3)在(2)的条件下,连接BC′,直接写出线段BC′的长.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先根据勾股定理知AB=2![]() ,再由轴对称性质知AC=AC′=2,据此可得答案;
,再由轴对称性质知AC=AC′=2,据此可得答案;
(2)先轴对称性质知AC=AC′=2,PC=PC′=1,∠AC′P=90°,作C′M⊥直线m,延长MC′交BC于点N可得四边形ACNM是矩形,设C′N=x,则MC′=2﹣x,证△AMC′∽△C′NP得![]() ,据此可得AM=2x,PN=
,据此可得AM=2x,PN=![]() ,根据AM=CN=CP+PN可得x=
,根据AM=CN=CP+PN可得x=![]() ,从而得出C′N=
,从而得出C′N=![]() ,C′M=
,C′M=![]() ,AM=
,AM=![]() ,PN=
,PN=![]() ,再证△DMC′∽△PNC′得
,再证△DMC′∽△PNC′得![]() ,据此求得DM=
,据此求得DM=![]() ,最后利用三角形面积公式求解可得答案;
,最后利用三角形面积公式求解可得答案;
(3)由(2)知PB=3,PN=![]() ,C′N=
,C′N=![]() ,据此求得BN=PB﹣PN=
,据此求得BN=PB﹣PN=![]() ,利用勾股定理可得答案.
,利用勾股定理可得答案.
(1)∵AC=2,BC=4,∠ACB=90°,
∴AB=![]() ,
,
∵△APC与△APC′关于直线AP对称,
∴AC=AC′=2,
则BC′=AB﹣AC′=2![]() ﹣2;
﹣2;
(2)∵PC=![]() BC,BC=4,
BC,BC=4,
∴PC=1,BP=3,
∵△APC与△APC′关于直线AP对称,
∴AC=AC′=2,PC=PC′=1,∠AC′P=90°,
如图,过点C′作C′M⊥直线m,延长MC′交BC于点N,
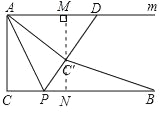
∵AD∥BC,
∴MN⊥BC,
则∠AMC′=∠C′NP=90°,
∴四边形ACNM是矩形,
∴AC=MN=2,AM=CN,
又∠AC′P=90°,
∴△AMC′∽△C′NP,
∴![]() ,
,
设C′N=x,则MC′=2﹣x,
∴![]() ,
,
解得AM=2x,PN=![]() ,
,
由AM=CN=CP+PN可得2x=1+![]() ,解得x=
,解得x=![]() ,
,
则C′N=![]() ,C′M=
,C′M=![]() ,AM=
,AM=![]() ,PN=
,PN=![]() ,
,
∵AD∥BC,
∴△DMC′∽△PNC′,
∴![]() ,即
,即![]() ,
,
解得:DM=![]() ,
,
∴AD=AM+DM=![]() ,
,
∴△ADC′面积为![]() ;
;
(3)由(2)知PB=3,PN=![]() ,C′N=
,C′N=![]() ,
,
∴BN=PB﹣PN=![]() ,
,
在Rt△BC′N中,BC′=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折, 使点A落在BC边上的点F处,则CE的最大值为( )

A.
B.
C.4
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.
进球数(个)
8
7
6
5
4
3
人数
2
1
4
7
8
2
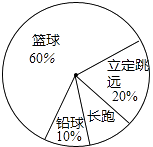
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为个;进球数的中位数为个,众数为个;
(2)该班共有多少学生;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
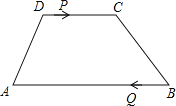
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱ABC-A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为 .
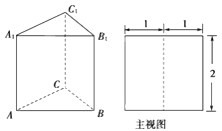
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:我们把分一条线段为两条相等线段的点称为线段的中点.如图1所示,则称点M为线段AB的中点.
问题解决:
(1)如图2所示,点A、B、C、D、E在数轴上的对应的数分别为﹣2、﹣1、0、1、2,则图2中,线段AC的中点是点 ,点C是线段 和线段 的中点,线段AB的中点对应的数是 ,线段BE的中点对应的数是 ;
(2)如图3,点E、F对应的数分别是e、f,则线段EF的中点对应的数为 (用含e、f的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC .
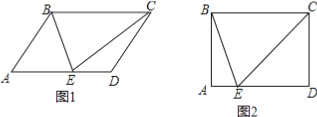
(1)如图1,判断△BCE的形状,并说明理由;
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长.
相关试题

