【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
参考答案:
【答案】(1)a=86,b=85,c=85;(2)八(2)班前5名同学的成绩较好,理由见解析.
【解析】
(1)根据平均数、中位数、众数的概念进行解答即可;
(2)根据它们的方差进行判断即可解答本题.
(1)a=![]() ,
,
将八(1)的成绩排序77、85、85、86、92,
可知中位数是85,众数是85,
所以b=85,c=85;
(2)∵22.8>19.2,
∴八(2)班前5名同学的成绩较好.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两种不同的数对处理器
 、
、 .当数对
.当数对 输入处理器
输入处理器 时,输出数对
时,输出数对 ,记作
,记作 ,
, ,
, ;但数对
;但数对 输入处理器
输入处理器 时,输出数对
时,输出数对 ,记作
,记作 ,
, ,
, .
.(1)
 ,
, ( , ),
( , ), ,
, ( , ).
( , ).(2)当
 ,
, ,
, 时,求
时,求 ,
, ;
;(3)对于数对
 ,
, ,
, ,
, 一定成立吗?若成立,说明理由;若不成立,举例说明.
一定成立吗?若成立,说明理由;若不成立,举例说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1,P2是点P关于AB、AC的对称点,连结P1P2,分别交AB、AC于点D、E.
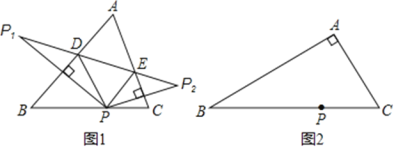
(1)若∠A=52°,求∠DPE的度数;
(2)如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、P2,(不写作法,保留作图痕迹),试判断点P1,P2与点A是否在同一直线上,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.
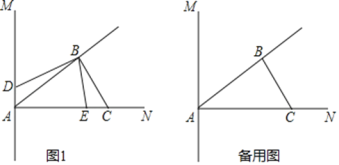
(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;
(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC全等?若存在,请求出时间t的值;若不存在,请说出理由.
-
科目: 来源: 题型:
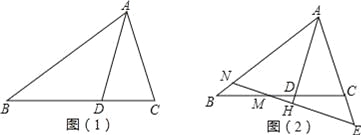
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B= °,∠C= °;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
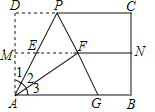
查看答案和解析>>【题目】如图,对折矩形纸片ABCD,使AB与DC重合,得到折痕MN,将纸片展平;再一次折叠,使点D落到MN上的点F处,折痕AP交MN于E;延长PF交AB于G.求证:
(1)△AFG≌△AFP;
(2)△APG为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,则( )
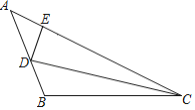
A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣
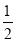 β
βC.∠AED=90°﹣α+βD.∠AED=90°+α+
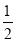 β
β
相关试题

