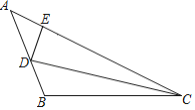
【题目】如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,则( )
A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣![]() β
β
C.∠AED=90°﹣α+βD.∠AED=90°+α+![]() β
β
参考答案:
【答案】A
【解析】
在AC上截取CF=BC,根据全等三角形的性质可得BD=DF=DE,可得∠AED=∠ABC,根据三角形的内角和可求解.
解:如图,在AC上截取CF=BC,
∵CF=BC,∠ACD=∠BCD,CD=CD,
∴△BDC≌△FDC(SAS)
∴∠ABC=∠CFD,DF=BD
∵BD=DE
∴DE=DF
∴∠DEF=∠DFE,
∴∠AED=∠CFD
∴∠AED=∠DBC=180°-∠A-∠ACB=180°-α-β
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级
平均分
中位数
众数
方差
八(1)
85
b
c
22.8
八(2)
a
85
85
19.2
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
-
科目: 来源: 题型:
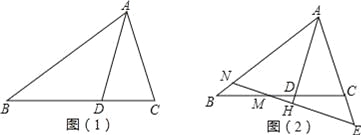
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B= °,∠C= °;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
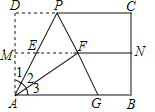
查看答案和解析>>【题目】如图,对折矩形纸片ABCD,使AB与DC重合,得到折痕MN,将纸片展平;再一次折叠,使点D落到MN上的点F处,折痕AP交MN于E;延长PF交AB于G.求证:
(1)△AFG≌△AFP;
(2)△APG为等边三角形.
-
科目: 来源: 题型:
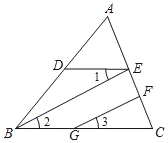
查看答案和解析>>【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究函数y=x+
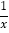 (x>0)与y=x+
(x>0)与y=x+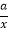 (x>0,a>0)的相关性质.
(x>0,a>0)的相关性质.(1)小聪同学对函数y=x+
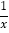 (x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
(x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;x
…
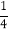


1

2

3
…
y
…
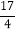
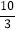

2
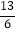

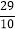
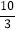
…
(2)请用配方法求函数y=x+
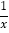 (x>0)的最小值;
(x>0)的最小值;(3)猜想函数y=x+
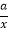 (x>0,a>0)的最小值为 .
(x>0,a>0)的最小值为 .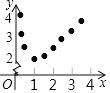
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
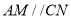 ,点
,点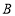 为平面内一点,
为平面内一点,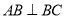 于
于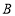 .
.(1)如图1,直接写出
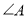 和
和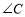 之间的数量关系 ;
之间的数量关系 ;(2)如图2,过点
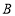 作
作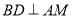 于点
于点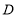 ,求证:
,求证: ;
;(3)如图3,在(2)问的条件下,点
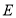 、
、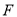 在
在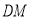 上,连接
上,连接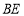 、
、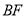 、
、 ,
,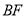 平分
平分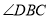 ,
,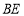 平分
平分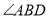 ,若
,若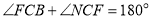 ,
,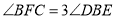 ,求
,求 的度数.
的度数.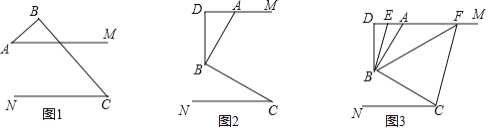
相关试题

