搜索
【题目】如图，在
中，
，
于点
，点
在
边上，且
，连接
、
、
．若
，求
的度数．
证明：∵
∴
（____________________________）
在和
中，
∴
（____________________________）
∴
______________（____________________________）
∵在中，
，
∴___________
_________
∵，
∴________________
∴
（ ）
参考答案：
【答案】垂直的定义，AB=CB，BE=BD，SAS，∠BDC，全等三角形的对应角相等，∠CAE，∠ACE，75°，等量代换．
【解析】
由
证明
．得出
（全等三角形的对应角相等）．由三角形的外角性质得出
．由已知求出
．即可得出答案．
解：
（垂直的定义）
在
和
中，
，
．
（全等三角形的对应角相等）．
在
中，
，
．
，
，
．
（等量代换
．
故答案为：垂直的定义，
，
，，
，全等三角形的对应角相等，
，
，
，等量代换．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列等式：
第一个等式：
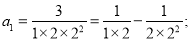
第二个等式：
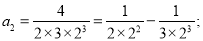
第三个等式：
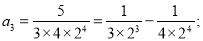
第四个等式：
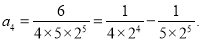
则式子
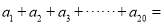__________________；用含n的代数式表示第n个等式：
____________________________； -
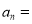科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的顶点分别为A（2，4），B（﹣2，2），C（3，1）．
（1）作出△ABC关于x轴对称的图形△DEF，写出顶点D、E、F的坐标．
（2）如果点H（3m﹣1，n﹣6）与点H′（2n+7，3m﹣9）关于y轴对称，求m，n的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=x2﹣2x﹣3，点P在该函数的图象上，点P到x轴、y轴的距离分别为d1、d2 ． 设d=d1+d2 ， 下列结论中： ①d没有最大值；
②d没有最小值；
③﹣1＜x＜3时，d随x的增大而增大；
④满足d=5的点P有四个．
其中正确结论的个数有（ ）
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米．甲同学先步行600米，然后乘公交车去学校、乙同学骑自行车去学校．已知甲步行速度是乙骑自行车速度的
，公交车的速度是乙骑自行车速度的2倍．甲乙两同学同时从家发去学校，结果甲同学比乙同学早到2分钟．（1）求乙骑自行车的速度；
（2）当甲到达学校时，乙同学离学校还有多远？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果两个三角形的两条边对应相等，夹角互补，那么这两个三角形叫做互补三角形，如图2，分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF，则图中的两个三角形就是互补三角形．
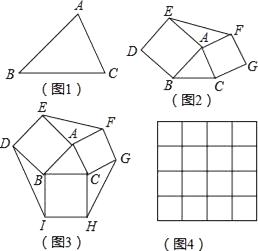
（1）用尺规将图1中的△ABC分割成两个互补三角形；
（2）证明图2中的△ABC与△AEF两个互补三角形面积相等；
（3）如图3，在图2的基础上再以BC为边向外作正方形BCHI．
①已知三个正方形面积分别是17、13、10，在如图4的网格中（网格中每个小正方形的边长为1）画出边长为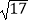
、 
、 
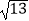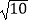的三角形，并计算图3中六边形DEFGHI的面积．
②若△ABC的面积为2，求以EF、DI、HG的长为边的三角形面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，正方形ABCD的边长为8，⊙O经过点C和点D，且与AB相切于点E．
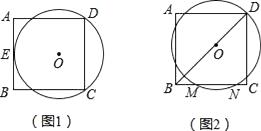
（1）求⊙O的半径；
（2）如图2，平移⊙O，使点O落在BD上，⊙O经过点D，BC与⊙O交于M，N，求MN2的值．
相关试题
