【题目】如图1,正方形ABCD的边长为8,⊙O经过点C和点D,且与AB相切于点E.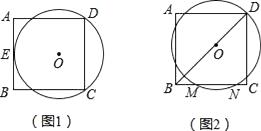
(1)求⊙O的半径;
(2)如图2,平移⊙O,使点O落在BD上,⊙O经过点D,BC与⊙O交于M,N,求MN2的值.
参考答案:
【答案】
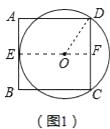
(1)解:连接EO,延长EO交CD于F,连接DO,设半径为x.
∵AB切○O于E,
∴EF⊥AB,
∵AB∥CD,
∴EF⊥CD,
∴∠OFD=90°,
在Rt△DOF中,∵∠OFD=90°,OF2+DF2=OD2,
∴x2=(8﹣x)2+42,
∴x=5,
∴⊙O的半径为5
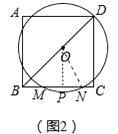
(2)解:如图2中,作OP⊥BC于P,连接ON,则OD=ON=5,
∵四边形ABCD是正方形,
∴BD=8 ![]() ,OB=BD﹣OD=8
,OB=BD﹣OD=8 ![]() ﹣5,OP=
﹣5,OP= ![]() =8﹣
=8﹣ ![]() ,
,
∴PN2=ON2﹣OP2=52﹣(8﹣ ![]() )2=40
)2=40 ![]() ﹣51.5,
﹣51.5,
∵MN=2PN,
∴MN2=4PN2=4(40 ![]() ﹣51.5)=160
﹣51.5)=160 ![]() ﹣206
﹣206
【解析】(1)连接EO,延长EO交CD于F,连接DO,设半径为x.根据切线的性质知EF⊥AB,根据平行线的性质及垂直的定义得出∠OFD=90°,在Rt△DOF中利用勾股定理列出方程求出解,即得到该圆的半径;
(2)如图2中,作OP⊥BC于P,连接ON,根据同圆的半径相等得OD=ON=5,根据正方形的性质及勾股定理得出BD的长,进而得出OB,根据平行线分线段成比例得出OP的长,根据勾股定理得出PN2=ON2﹣OP2,从而列出方程求出PN的长,最后根据垂径定理得出MN的长算出答案。
【考点精析】通过灵活运用平行线的判定与性质和正方形的性质,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 于点
于点 ,点
,点 在
在 边上,且
边上,且 ,连接
,连接 、
、 、
、 .若
.若 ,求
,求 的度数.
的度数.
证明:∵

∴
 (____________________________)
(____________________________)在
 和
和 中,
中,
∴
 (____________________________)
(____________________________)∴
 ______________(____________________________)
______________(____________________________)∵在
 中,
中, ,
,
∴
 ___________
___________ _________
_________∵
 ,
,
∴
 ________________
________________∴
 ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的
 ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.
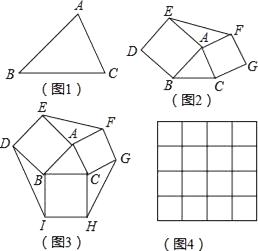
(1)用尺规将图1中的△ABC分割成两个互补三角形;
(2)证明图2中的△ABC与△AEF两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI.
①已知三个正方形面积分别是17、13、10,在如图4的网格中(网格中每个小正方形的边长为1)画出边长为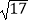 、
、 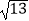 、
、 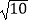 的三角形,并计算图3中六边形DEFGHI的面积.
的三角形,并计算图3中六边形DEFGHI的面积.
②若△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积. -
科目: 来源: 题型:
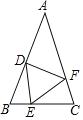
查看答案和解析>>【题目】如图,在△ABC中AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)猜想:当∠A为多少度时,∠DEF=60°?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A. 2,
 B. 2,1 C. 4,
B. 2,1 C. 4, D. 4,3
D. 4,3
相关试题

