【题目】如图,已知直线AB∥CD∥EF,∠POQ=90°,它的顶点O在CD上,两边分别与AB、EF相交于点P、点Q,射线OC始终在∠POQ的内部.
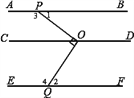
(1)求∠1+∠2的度数;
(2)直接写出∠3与∠4的数量关系;
(3)若∠POQ的度数为α,且0°<α<180°,其余条件不变,猜想∠3与∠4的数量关系(用含α的式子表示);并说明理由.
参考答案:
【答案】(1)∠1+∠2=90°;(2)∠3+∠4=270°;(3)∠3+∠4=360°-α, 理由见解析.
【解析】试题分析:(1)由AB与CD平行,利用两直线平行得到一对内错角相等,由CD与EF平行,同理得到一对内错角相等,而∠POQ=∠POC+∠QOC=90°,等量代换即可求出∠1+∠2的度数;
(2)由∠APB与∠EQF为两个平角,得到∠1+∠3+∠4+∠2=360°,由(1)求出的∠1+∠2的度数即可得到∠3+∠4的度数;
(3)由AB与CD平行,利用两直线平行得到一对内错角相等,由CD与EF平行,同理得到一对内错角相等,而∠POQ=∠POC+∠QOC=90°,等量代换即可求出∠1+∠2=α,由∠APB与∠EQF为两个平角,得到∠1+∠3+∠4+∠2=360°,由∠1+∠2=α即可得到∠3+∠4的度数.
试题解析:(1)∵AB∥CD,
∴∠1=∠POC,
∵CD∥EF,
∴∠2=∠QOC,
∵∠POQ=∠POC+∠QOC=90°,
∴∠1+∠2=90°;
(2)∵∠1+∠3=180°,∠4+∠2=180°,
∴∠1+∠3+∠4+∠2=360°,
又∵∠1+∠2=90°,
∴∠3+∠4=270°;
(3))∵AB∥CD,
∴∠1=∠POC,
∵CD∥EF,
∴∠2=∠QOC,
∵∠POQ=∠POC+∠QOC=α,
∴∠1+∠2=α;
∵∠1+∠3=180°,∠4+∠2=180°,
∴∠1+∠3+∠4+∠2=360°,
又∵∠1+∠2=α,
∴∠3+∠4=360°-α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学想利用木条为七年级数学组制作一个三角形的工具,那么下列哪组数据的三根木条的长度能符合他的要求?( )
A、4,2,2 B、3,6,6 C、2,3,6 D、7,13,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长分别为3cm和8cm,则这个三角形的第三边的长可能是( )
A. 4cm B. 5cm C. 6cm D. 13cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和与它的外角和相等,则这个多边形是( )
A.三角形
B.四边形
C.五边形
D.六边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:

∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.
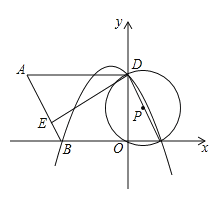
(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD各点的坐标分别为A(4,4),B(1,3),C(3,3),D(3,1),在同一方格纸中,
(1)将四边形ABCD向左平移4个单位长度,画出平移后的四边形
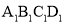 ,并写出各点的坐标;
,并写出各点的坐标;(2)将四边形ABCD绕原点O旋转180°,画出旋转后的图形四边形
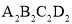 ,并写出各点的坐标.
,并写出各点的坐标.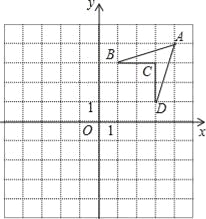
相关试题

