【题目】如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线![]() 恰好经过边AB的四等分点E(BE<AE),则k的值为____________.
恰好经过边AB的四等分点E(BE<AE),则k的值为____________.

参考答案:
【答案】-![]()
【解析】
由AD∥BC,可得出S△BCD=S△BCA、S△ACD=S△ABD,根据△ACD与△BCD的面积分别为10和20结合同底三角形面积的性质,即可得出AO:OC=DO:OB=1:2,进而可得出S△AOB=![]() ,再根据反比例函数系数k的几何意义以及相似三角形的性质得出|k|=
,再根据反比例函数系数k的几何意义以及相似三角形的性质得出|k|=![]() ,解之即可得出结论.
,解之即可得出结论.
∵AD∥BC,
∴S△BCD=S△BCA,S△ACD=S△ABD.
∵△ACD与△BCD的面积分别为10和20,
∴△ABD和△BCD面积比为1:2,
∴根据同底得:AO:OC=DO:OB=1:2,
∴S△AOB=![]() .
.
∵双曲线![]() 恰好经过边AB的四等分点E(BE<AE),
恰好经过边AB的四等分点E(BE<AE),
∴![]() S△AOB+|k|+
S△AOB+|k|+![]() S△AOB=S△AOB,
S△AOB=S△AOB,
∴|k|=![]() S△AOB=
S△AOB=![]() ,
,
∵双曲线经过第二象限,k<0,
∴k=-![]() .
.
故答案为-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究)
(1)观察下列算式,并完成填空:
1=12
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+…+(2n-1)=______.(n是正整数)
(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
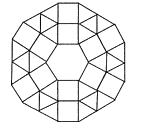
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第n层中含有______块正三角形地板砖(用含n的代数式表示).
(应用)
该市打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
-
科目: 来源: 题型:
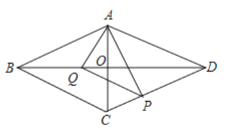
查看答案和解析>>【题目】菱形
 中,对角线
中,对角线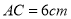 ,
,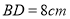 ,动点
,动点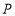 、
、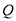 分别从点
分别从点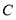 、
、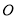 同时出发,运动速度都是
同时出发,运动速度都是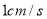 ,点
,点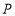 由
由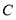 向
向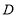 运动;点
运动;点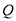 由
由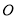 向
向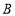 运动,当
运动,当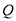 到达点
到达点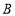 时,
时,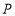 ,
,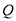 两点运动停止,设时间为
两点运动停止,设时间为 秒
秒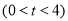 .连接
.连接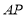 ,
,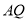 ,
, .
.
(1)当
 为何值时,
为何值时,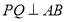 ;
;(2)设
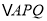 的面积为
的面积为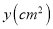 ,请写出
,请写出 与
与 的函数关系式;
的函数关系式;(3)当
 为何值时,
为何值时,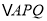 的面积是四边形
的面积是四边形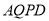 面积的
面积的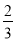 ;
;(4)是否存在
 值,使得线段
值,使得线段 经过
经过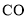 的中点
的中点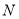 ;若存在,求出
;若存在,求出 值;若不存在,请说明理由.
值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,若要使四边形EFGH为菱形,则还需增加的条件是( )
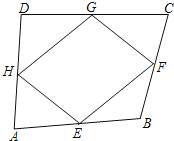
A.AC=BDB.AC⊥BDC.AC⊥BD且AC=BDD.AB=AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(4,0),B(4,4),点P在半径为2的圆O上运动,则
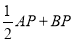 的最小值为____________.
的最小值为____________. 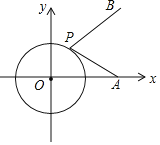
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,试判定四边形DEBF是何种特殊四边形?并说明理由.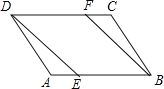
-
科目: 来源: 题型:
查看答案和解析>>【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
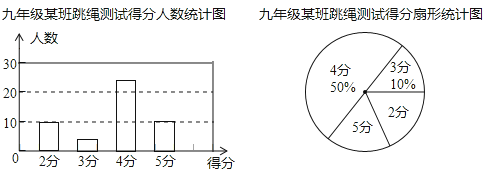
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行了第二次测试,测得成绩的最低分为3分.且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
相关试题

