【题目】(探究)
(1)观察下列算式,并完成填空:
1=12
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+…+(2n-1)=______.(n是正整数)
(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
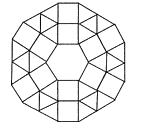
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第n层中含有______块正三角形地板砖(用含n的代数式表示).
(应用)
该市打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
参考答案:
【答案】【探究】n2;(2)① 6,30;②6(2n-1)或12n-6;【应用】铺设这样的图案,最多能铺8层,理由见解析
【解析】
一.探究(1)观察算式规律,1+3+5+…+(2n-1)=n2;
(2)①第一层6块正方形和6块正三角形地板砖,第二层6块正方形和6+12=18块正三角形地板砖,第三层6块正方形和18+12=30块正三角形地板砖;
②第一层6=6×1=6×(2×1-1)块正三角形地板砖,第二层18=6×3=6×(2×2-1)块正三角形地板砖,第三层30=6×5=6×(2×3-1)块正三角形地板砖,第n层6=6×1=6(2n-1)块正三角形地板砖,
二.应用
150块正方形地板砖可以铺设这样的图案150÷6=25(层),铺设n层需要正三角形地板砖的数量为:6[1+3+5+…+(2n-1)]=6n2,6n2=420,n2=70,n=![]() ,8<n<9,所以420块正三角形地板砖最多可以铺设这样的图案8层.因此铺设这样的图案,最多能铺8层.
,8<n<9,所以420块正三角形地板砖最多可以铺设这样的图案8层.因此铺设这样的图案,最多能铺8层.
解:一.探究
(1)观察算式规律,1+3+5+…+(2n-1)=n2,
故答案为n2;
(2)①∵第一层包括6块正方形和6块正三角形地板砖,
第二层包括6块正方形和6+12=18块正三角形地板砖,
∴第三层包括6块正方形和18+12=30块正三角形地板砖,
故答案为6,30;
②∵第一层6=6×1=6×(2×1-1)块正三角形地板砖,
第二层18=6×3=6×(2×2-1)块正三角形地板砖,
第三层30=6×5=6×(2×3-1)块正三角形地板砖,
∴第n层6=6×1=6(2n-1)块正三角形地板砖,
故答案为6(2n-1)或12n-6.
二.应用
铺设这样的图案,最多能铺8层.
理由如下:
∵150÷6=25(层),
∴150块正方形地板砖可以铺设这样的图案25层;
∵铺设n层需要正三角形地板砖的数量为:6[1+3+5+…+(2n-1)]=6n2,
∴6n2=420,n2=70,n=![]() .
.
又∵8<![]() <9,即8<n<9,
<9,即8<n<9,
∴420块正三角形地板砖最多可以铺设这样的图案8层.
∴铺设这样的图案,最多能铺8层.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某果品超市经销一种水果,已知该水果的进价为每千克15元,通过一段时间的销售情况发现,该种水果每周的销售总额相同,且每周的销售量
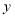 (千克)与每千克售价
(千克)与每千克售价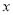 (元)的关系如表所示:
(元)的关系如表所示:每千克售价
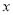 (元)
(元)25
30
40
每周销售量
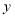 (千克)
(千克)240
200
150
(1)求出每周销售量
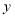 (千克)与每千克售价
(千克)与每千克售价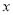 (元)的函数关系式.
(元)的函数关系式.(2)由于销售淡季即将来临,超市要完成每周销售量不低于300千克的任务,则该种水果每千克售价最多定为多少元?
(3)在(2)的基础上,超市销售该种水果能否达到每周获利2000元?说明理由.
-
科目: 来源: 题型:
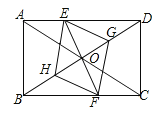
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜坡AB长10米,按图中的直角坐标系可用
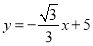 表示,点A,B分别在x轴和y轴上,且
表示,点A,B分别在x轴和y轴上,且 .在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用
.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用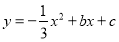 表示.
表示.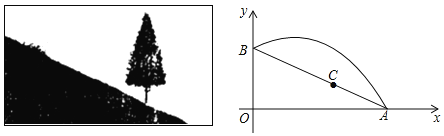
(1)求抛物线的函数关系式(不必写自变量取值范围);
(2)求水柱离坡面AB的最大高度;
(3)在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?
-
科目: 来源: 题型:
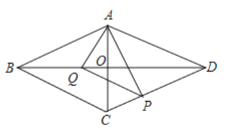
查看答案和解析>>【题目】菱形
 中,对角线
中,对角线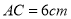 ,
,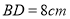 ,动点
,动点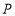 、
、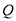 分别从点
分别从点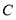 、
、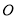 同时出发,运动速度都是
同时出发,运动速度都是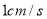 ,点
,点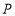 由
由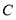 向
向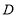 运动;点
运动;点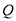 由
由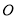 向
向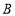 运动,当
运动,当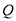 到达点
到达点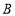 时,
时,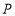 ,
,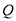 两点运动停止,设时间为
两点运动停止,设时间为 秒
秒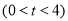 .连接
.连接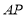 ,
,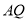 ,
, .
.
(1)当
 为何值时,
为何值时,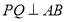 ;
;(2)设
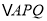 的面积为
的面积为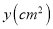 ,请写出
,请写出 与
与 的函数关系式;
的函数关系式;(3)当
 为何值时,
为何值时,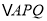 的面积是四边形
的面积是四边形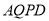 面积的
面积的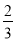 ;
;(4)是否存在
 值,使得线段
值,使得线段 经过
经过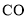 的中点
的中点 ;若存在,求出
;若存在,求出 值;若不存在,请说明理由.
值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,若要使四边形EFGH为菱形,则还需增加的条件是( )
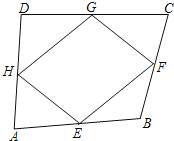
A.AC=BDB.AC⊥BDC.AC⊥BD且AC=BDD.AB=AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线
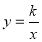 恰好经过边AB的四等分点E(BE<AE),则k的值为____________.
恰好经过边AB的四等分点E(BE<AE),则k的值为____________.
相关试题

