【题目】菱形![]() 中,对角线
中,对角线![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,运动速度都是
同时出发,运动速度都是![]() ,点
,点![]() 由
由![]() 向
向![]() 运动;点
运动;点![]() 由
由![]() 向
向![]() 运动,当
运动,当![]() 到达点
到达点![]() 时,
时,![]() ,
,![]() 两点运动停止,设时间为
两点运动停止,设时间为![]() 秒
秒![]() .连接
.连接![]() ,
,![]() ,
,![]() .
.
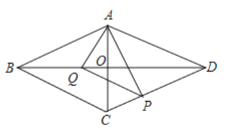
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)设![]() 的面积为
的面积为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() 的面积是四边形
的面积是四边形![]() 面积的
面积的![]() ;
;
(4)是否存在![]() 值,使得线段
值,使得线段![]() 经过
经过![]() 的中点
的中点![]() ;若存在,求出
;若存在,求出![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
参考答案:
【答案】(1)t=1;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)如图3中,作CH⊥AB于H交BD于M.由PQ∥CM,可得![]() ,由此构建方程即可解决问题;
,由此构建方程即可解决问题;
(2)如图1中,作AM⊥CD于M,PH⊥BD于H.根据y=S△ADQ+S△PDQ-S△ADP,计算即可解决问题;
(3)由△APQ的面积是四边形AQPD面积的![]() ,推出S△APQ=2S△APD,由此构建方程即可解决问题;
,推出S△APQ=2S△APD,由此构建方程即可解决问题;
(4)如图4中,作PH⊥AC于H.由OQ∥PH,ON=NC=![]() ,可得
,可得![]() ,由此构建方程即可解决问题;
,由此构建方程即可解决问题;
解:(1)如图3中,作CH⊥AB于H交BD于M.
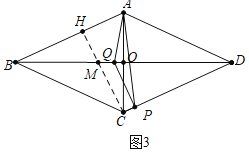
易知CH=![]() ,AH=
,AH=![]()
∵∠MCO=∠ACH,∠COM=∠CHA=90°,
∴△COM∽△CHA,
∴![]() ,
,
∴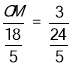 ,
,
∴OM=![]() ,
,
∵PQ⊥AB,CH⊥AB,
∴PQ∥CM,
∴![]() ,
,
∴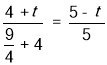 ,
,
∴t=1,
∴t=1s时,PQ⊥AB.
(2)如图1中,作AM⊥CD于M,PH⊥BD于H.
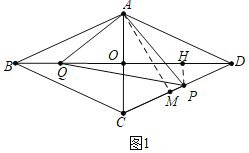
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=3,OB=OD=4,
∴∠COD=90°,
∴CD=![]() =5,
=5,
∵![]() ACOD=
ACOD=![]() CDAM,
CDAM,
∴AM=![]() ,
,
∵OQ=CP=t,
∴DQ=4+t.PD=5-t.
∵PH∥OC,
∴![]()
∴![]() ,
,
∴PH=![]() (5-t),
(5-t),
∴y=S△ADQ+S△PDQ-S△ADP
=![]() (4+t)3+
(4+t)3+![]() (4+t)
(4+t)![]() (5-t)-
(5-t)-![]() (5-t)
(5-t)![]()
=-![]() t2+
t2+![]() t(0<t≤4).
t(0<t≤4).
(3)如图2中,
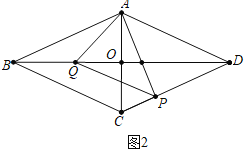
∵△APQ的面积是四边形AQPD面积的![]() ,
,
∴S△APQ=2S△APD,
∴-![]() t2+
t2+![]() t=2
t=2![]() (5-t)
(5-t)![]() ,
,
解得t=15-![]() 或15+
或15+![]() (舍弃),
(舍弃),
∴t=15-![]() 时,△APQ的面积是四边形AQPD面积的
时,△APQ的面积是四边形AQPD面积的![]() .
.
(4)如图4中,作PH⊥ACspan>于H.
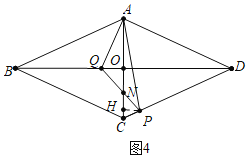
∵OQ∥PH,ON=NC=![]() ,
,
∴![]() ,
,
∴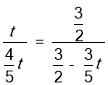 ,
,
∴t=![]() ,
,
∴t=![]() 时,PQ经过线段OC的中点N.
时,PQ经过线段OC的中点N.
-
科目: 来源: 题型:
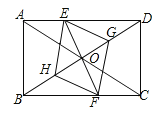
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,点E在边AD上,点F在边BC上,且AE=CF,作EG∥FH,分别与对角线BD交于点G、H,连接EH,FG.
(1)求证:△BFH≌△DEG;
(2)连接DF,若BF=DF,则四边形EGFH是什么特殊四边形?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜坡AB长10米,按图中的直角坐标系可用
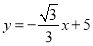 表示,点A,B分别在x轴和y轴上,且
表示,点A,B分别在x轴和y轴上,且 .在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用
.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用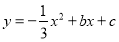 表示.
表示.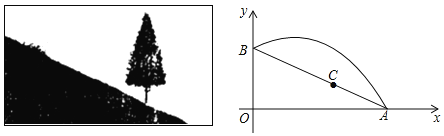
(1)求抛物线的函数关系式(不必写自变量取值范围);
(2)求水柱离坡面AB的最大高度;
(3)在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究)
(1)观察下列算式,并完成填空:
1=12
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+…+(2n-1)=______.(n是正整数)
(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
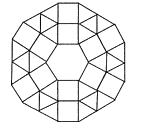
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第n层中含有______块正三角形地板砖(用含n的代数式表示).
(应用)
该市打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,若要使四边形EFGH为菱形,则还需增加的条件是( )
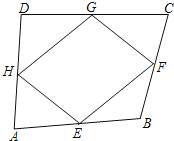
A.AC=BDB.AC⊥BDC.AC⊥BD且AC=BDD.AB=AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的顶点都在坐标轴上,若AD∥BC,△ACD与△BCD的面积分别为10和20,若双曲线
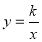 恰好经过边AB的四等分点E(BE<AE),则k的值为____________.
恰好经过边AB的四等分点E(BE<AE),则k的值为____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(4,0),B(4,4),点P在半径为2的圆O上运动,则
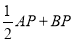 的最小值为____________.
的最小值为____________. 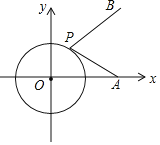
相关试题

