【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动.已知点A的速度是1单位长度/秒,点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
(1)求请在数轴上标出A、B两点从原点出发运动3秒时的位置;
![]()
(2)若A、B两点在(1)中的位置,数轴上是否存在一点P到点A,点B的距离之和为16,并求出此时点P表示的数;若不存在,请说明理由.
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以10单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
参考答案:
【答案】(1)点A表示的数为﹣3,点B表示的数为12,图见解析;(2)数轴上存在一点P到点A,点B的距离之和为16,此时点P表示的数为﹣![]() 或
或![]() ;(3)点C从开始运动到停止运动,行驶的路程是50个单位长度.
;(3)点C从开始运动到停止运动,行驶的路程是50个单位长度.
【解析】
(1)由点A,B的运动速度、运动方向及运动时间,可求出出发运动3秒时点A,B表示的数;
(2)设点P表示的数为x,分x<﹣3,﹣3≤x≤12及x>12三种情况考虑,由PA+PB=16,即可得出关于x的一元一次方程,解之即可得出结论;
(3)设点B需用t秒钟才可追上点A,根据两点的速度之差×运动时间=两点间的距离,即可得出关于t的一元一次方程,解之即可得出t值,再结合点C的运动速度,即可求出点C从开始运动到停止运动行驶的路程.
解:(1)∵﹣1×3=﹣3,4×3=12,
∴出发运动3秒时,点A表示的数为﹣3,点B表示的数为12,
将其标记在数轴上,如图所示;
![]()
(2)设点P表示的数为x.
当x<﹣3时,(﹣3﹣x)+(12﹣x)=16,
解得:x=﹣![]() ;
;
当﹣3≤x≤12时,x﹣(﹣3)+(12﹣x)=15≠16,
∴方程无解;
当x>12时,x﹣(﹣3)+(x﹣12)=16,
解得:x=![]() ;
;
综上所述:数轴上存在一点P到点A,点B的距离之和为16,此时点P表示的数为﹣![]() 或
或![]() ;
;
(3)设点B需用t秒钟,才可追上点A,
根据题意得:(4﹣1)t=12﹣(﹣3),
解得:t=5,
∴10t=50.
答:点C从开始运动到停止运动,行驶的路程是50个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC 中,AB=AC,∠BAC=90°,D 是BC 上一点,EC⊥BC,EC=BD,DF=FE.
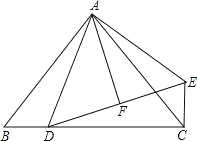
求证:(1)△ABD≌△ACE;
(2)AF⊥DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】之前我们学习了一元一次方程的解法,下面是一道解一元一次方程的题:
解方程
 ﹣
﹣ =1
=1老师说:这是一道含有分母的一元一次方程,我们可以根据等式的性质,可以把方程的两边同乘以6,这样就可以去掉分母了.于是,小明按照老师说的方法进行了解答,小明同学的解题过程如下:
解:方程两边同时乘以6,得
 ×6﹣
×6﹣ ×6=1…………①
×6=1…………①去分母,得:2(2﹣3x)﹣3(x﹣5)=1………②
去括号,得:4﹣6x﹣3x+15=1……………③
移项,得:﹣6x﹣3x=1﹣4﹣15…………④
合并同类项,得﹣9x=﹣18……………⑤
系数化1,得:x=2………………⑥
上述小明的解题过程从第 步开始出现错误,错误的原因是 .
请帮小明改正错误,写出完整的解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.若AE、CD为△ABC的角平分线.
(1)求证:∠AFC=120°;
(2)若AD=6,CE=4,求AC的长?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=
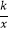 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )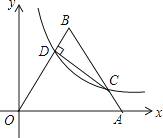
A.25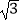
B.18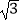
C.9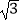
D.9
相关试题

