【题目】阅读下面材料:小明遇到这样一个问题;△ABC中,有两个内角相等.
①若∠A=110°,求∠B的度数;
②若∠A=40°,求∠B的度数.
小明通过探究发现,∠A的度数不同,∠B的度数的个数也可能不同,因此为同学们提供了如下解题的想法:
对于问题①,根据三角形内角和定理,∵∠A=110°>90°,∠B=∠C=35°;
对于问题②,根据三角形内角和定理,∵∠A=40°<90°,∴∠A=∠B或∠A=∠C或∠B=∠C,∴∠B的度数可求.请回答:
(1)问题②中∠B的度数为 ;
(2)参考小明解决问题的思路,解决下面问题:
△ABC中,有两个内角相等.设∠A=x°,当∠B有三个不同的度数时,求∠B的度数(用含x的代式表示)以及x的取值范围.
参考答案:
【答案】(1)40°或70°或100°;(2)∠B=x°或180°﹣2x°或90°﹣![]() x°,x的取值范围是0<x<90且x≠60.
x°,x的取值范围是0<x<90且x≠60.
【解析】
(1)根据三角形内角和定理即可求出答案.
(2)由(1)问的解答过程可类比求出x的取值范围.
解:(1)当∠A=∠B时,
∴∠B=40°,
当∠A=∠C=40°时,
∴∠B=180﹣∠A﹣∠C=100°,
当∠B=∠C时,
∴![]()
故∠B的度数为40°或70°或100°
(2)当0<x<90时,∠B的度数有三个,
当∠A=∠B时,∠B=x°,
当∠A=∠C时,
∵∠A+∠B+∠C=180°,
∴∠B=180﹣2x°,
当∠B=∠C时,
∵∠A+∠B+∠C=180°,
∴![]()
∵![]()
∴x≠60
∴∠B=x°或180°﹣2x°或![]()
x的取值范围是0<x<90且x≠60
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:
①b2﹣4ac=0;②a+b+c>0;③2a﹣b=0;④c﹣a=3
其中正确的有( )个.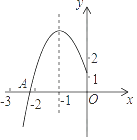
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】共有1500kg化工原料,由A,B两种机器人同时搬运,其中,A型机器人比B型机器每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,问需要多长时间才能运完?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图抛物线y=ax2+bx+c的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a= ;③ac=b﹣1;④
;③ac=b﹣1;④  >0
>0
其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店欲购进A、B两种品牌的足球进行销售,若购进A种品牌的足球50个,B种品牌的足球25个,需花费成本4250元;若购进A种品牌的足球15个,B种品牌的足球10个,需花费成本1450元.
(1)求购进A、B两种品牌的足球每个各需成本多少元;
(2)根据市场调研,A种品牌的足球每个售价90元,B种品牌的足球每个售价120元,该体育用品商店购进A、B两种品牌的足球进行销售,恰好用了7000元的成本.正值俄罗斯世界怀开赛,为了回馈新老顾客,决定A品牌足球按售价降低20元出售,B品牌足球按售价的7折出售,且保证利润不低于2000元,问A种品牌的足球至少购进多少个.
-
科目: 来源: 题型:
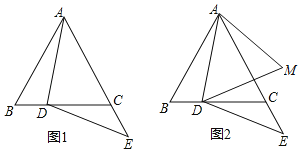
查看答案和解析>>【题目】在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)若点E关于直线BC的对称点为M(如图2),连接DM,AM.求证:DA=AM.
相关试题

