【题目】如图,直线y=kx+b经过点A(-5,0),B(-1,4)
(1)求直线AB的表达式;
(2)求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;
(3)根据图象,直接写出关于x的不等式kx+b>-2x-4的解集.

参考答案:
【答案】(1)y=x+5;(2)![]() ;(3)x>-3.
;(3)x>-3.
【解析】
(1)利用待定系数法求一次函数解析式即可;
(2)联立两直线解析式,解方程组可得到两直线交点C的坐标,即可求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;
(3)根据图形,找出点C右边的部分的x的取值范围即可.
解:(1)∵直线y=kx+b经过点A(-5,0),B(-1,4),
![]() ,解得
,解得![]() ,
,
∴直线AB的表达式为:y=x+5;
(2)∵若直线y= -2x-4与直线AB相交于点C,
∴![]() ,解得
,解得![]() ,故点C(-3,2).
,故点C(-3,2).
∵y= -2x-4与y=x+5分别交y轴于点E和点D,∴D(0,5),E(0,-4),
直线CE:y= -2x-4与直线AB及y轴围成图形的面积为:![]() DE|Cx|=
DE|Cx|=![]() ×9×3=
×9×3=![]() ;
;
(3)根据图象可得x>-3.
故答案为:(1)y=x+5;(2)![]() ;(3)x>-3.
;(3)x>-3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AE=3,ED=
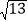 ,求BC的长度.
,求BC的长度.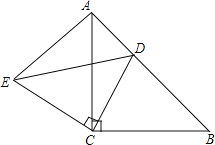
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于雾霾天气频发,市场上防护口罩出现热销.某药店准备购进一批
 两种不同型号口罩进行销售.下表是甲、乙两人购买
两种不同型号口罩进行销售.下表是甲、乙两人购买 两种型号口罩的情况:
两种型号口罩的情况:A型号数量(单位:个)
B型号数量(单位:个)
总售价(单位:元)
甲
1
3
26
乙
3
2
29
(1)求一个
 型口罩和一个
型口罩和一个 型口罩的售价各是多少元?
型口罩的售价各是多少元?(2)药店准备购进这两种型号的口罩共50个,其中
 型口罩数量不少于35个,且不多于
型口罩数量不少于35个,且不多于 型口罩的3倍,有几种购买方案?请写出购买方案.
型口罩的3倍,有几种购买方案?请写出购买方案.(3)在(2)的条件下,药店在销售完这批口罩后,总售价能否达到282元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
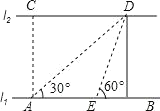
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
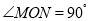 ,点
,点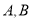 分别在射线
分别在射线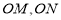 上运动(不与点
上运动(不与点 重合)
重合)观察:
(1)如图1,若
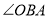 和
和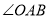 的平分线交于点
的平分线交于点 ,
,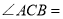 _____°
_____°
猜想:
(2)如图2,随着点
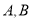 分别在射线
分别在射线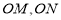 上运动(不与点
上运动(不与点 重合). 若
重合). 若 是
是 的平分线,
的平分线, 的反向延长线与
的反向延长线与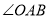 的平分线交于点
的平分线交于点 ,
, 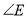 的大小会变吗?如果不会,求
的大小会变吗?如果不会,求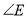 的度数;如果会改变,说明理由.
的度数;如果会改变,说明理由.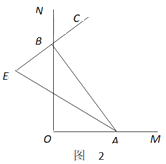
拓展:
(3)如图3,在(2)基础上,小明将
 沿
沿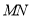 折叠,使点
折叠,使点 落在四边形
落在四边形 内点
内点 ′的位置,求
′的位置,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留一丝空隙,又不互相重叠(在数学上叫做平面镶嵌).这显然与正多边形的内角大小有关,当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请你根据图中的图形,填写表中空格:

正多边形边数
3
4
5
6
……
n
正多边形每个内角度数
60°
90°
108°
120°
……
(2)如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
相关试题

