【题目】在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留一丝空隙,又不互相重叠(在数学上叫做平面镶嵌).这显然与正多边形的内角大小有关,当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.
(1)请你根据图中的图形,填写表中空格:

正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
正多边形每个内角度数 | 60° | 90° | 108° | 120° | …… |
(2)如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?
参考答案:
【答案】(1)![]() (2) 正三角形、正四边形(或正方形)、正六边形
(2) 正三角形、正四边形(或正方形)、正六边形
【解析】
(1)利用正多边形一个内角=180-![]() 求解;
求解;
(2)进行平面镶嵌就是在同一顶点处的几个多边形的内角和应为360°,因此我们只需验证360°是不是上面所给的几个正多边形的一个内角度数的整数倍;
解:(1)由正n边形的内角的性质可分别求得正三角形、正方形、正五边形、正六边形…正n边形的每一个内角为:60°,90°,108°,120°,…![]() ;
;
(2)如限于用一种正多边形镶嵌,则由一顶点的周围角的和等于360°得正三角形、正四边形(或正方形)、正六边形都能镶嵌成一个平面图形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b经过点A(-5,0),B(-1,4)
(1)求直线AB的表达式;
(2)求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;
(3)根据图象,直接写出关于x的不等式kx+b>-2x-4的解集.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
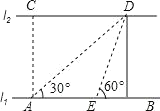
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
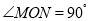 ,点
,点 分别在射线
分别在射线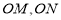 上运动(不与点
上运动(不与点 重合)
重合)观察:
(1)如图1,若
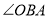 和
和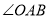 的平分线交于点
的平分线交于点 ,
,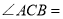 _____°
_____°
猜想:
(2)如图2,随着点
 分别在射线
分别在射线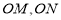 上运动(不与点
上运动(不与点 重合). 若
重合). 若 是
是 的平分线,
的平分线, 的反向延长线与
的反向延长线与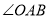 的平分线交于点
的平分线交于点 ,
, 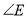 的大小会变吗?如果不会,求
的大小会变吗?如果不会,求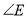 的度数;如果会改变,说明理由.
的度数;如果会改变,说明理由.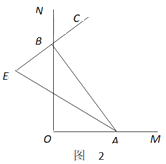
拓展:
(3)如图3,在(2)基础上,小明将
 沿
沿 折叠,使点
折叠,使点 落在四边形
落在四边形 内点
内点 ′的位置,求
′的位置,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
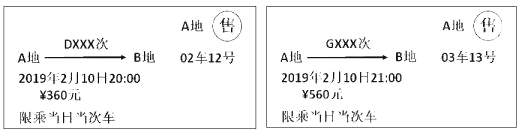
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副直角三角尺如图①叠放,先将含
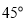 角的三角尺
角的三角尺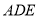 固定不动,含角
固定不动,含角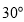 的三角尺
的三角尺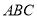 绕顶点
绕顶点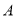 顺时针旋转
顺时针旋转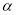 (
(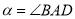 且
且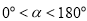 ),使两块三角尺至少有一组边平行.
),使两块三角尺至少有一组边平行.
完成下列任务:(温馨提示:先用你的三角尺拜摆一摆)
(1)填空:如图②,当
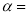 时
时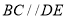 ,;
,;(2)请你分别在图③、图④中各画出一种符合要求的图形,标出
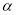 ,并完成下列问题:
,并完成下列问题:图③中,当
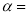 时,
时,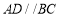 ;
;图④中,当
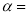 时,
时,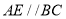 或者
或者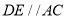 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是坐标原点,P(m,n)(m>0)是函数y=
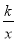 (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+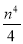 .
.(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3)设n是小于20的整数,且k≠
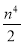 ,求OP2的最小值.
,求OP2的最小值.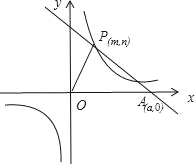
相关试题

