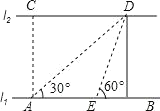
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
参考答案:
【答案】C、D两点间的距离为30m.
【解析】直接利用等腰三角形的判定与性质得出DE=AE=20,进而求出EF的长,再得出四边形ACDF为矩形,则CD=AF=AE+EF求出答案.
解:过点D作l1的垂线,垂足为F,
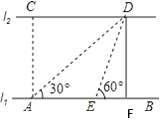
∵∠DEB=60°,∠DAB=30°,
∴∠ADE=∠DEB﹣∠DAB=30°,
∴△ADE为等腰三角形,
∴DE=AE=20,
在Rt△DEF中,EF=DEcos60°=20×![]() =10,
=10,
∵DF⊥AF,
∴∠DFB=90°,
∴AC∥DF,由已知l1∥l2,
∴CD∥AF,
∴四边形ACDF为矩形,CD=AF=AE+EF=30,
答:C、D两点间的距离为30m
“点睛”此题考查了两点之间的距离以及等腰三角形的判定与性质以及锐角三角函数关系,得出EF的长是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF。
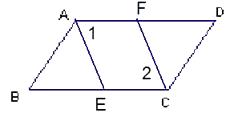
试说明:
(1)AE∥CF;
(2)AB∥CD。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D,DE⊥AB于点E,则EB的长是( )
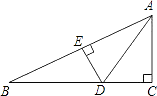
A.3 cm
B.4 cm
C.5 cm
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例.
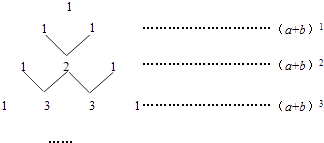
这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为( )
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列五个命题:①直径是弦,②优弧大于劣弧,③等弧的弧长相等,④平分弦的直径垂直于弦,⑤等弧所对的弦相等.其中正确的有( )个.
A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】设m,n分别为一元二次方程x2﹣2x﹣2022=0的两个实数根,则m2﹣3m﹣n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.
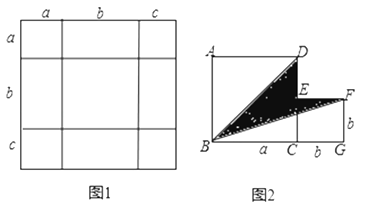
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
相关试题

