【题目】将直角边长为6的等腰直角△AOC放在平面直角坐标系中,点O为坐标原点,点C、A分别在x轴,y轴的正半轴上,一条抛物线经过点A、C及点B(﹣3,0).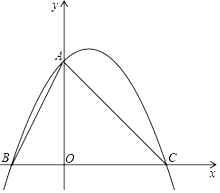
(1)求该抛物线的解析式;
(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;
(3)若点P(t,t)在抛物线上,则称点P为抛物线的不动点,将(1)中的抛物线进行平移,平移后,该抛物线只有一个不动点,且顶点在直线y=2x﹣ ![]() 上,求此时抛物线的解析式.
上,求此时抛物线的解析式.
参考答案:
【答案】
(1)
解:∵B(﹣3,0),C(6,0),设抛物线为y=a(x+3)(x﹣6),过A(0,6)
∴6=a(0+3)(0﹣6),
解得a=﹣ ![]() ,
,
∴y=﹣ ![]() (x+3)(x﹣6),
(x+3)(x﹣6),
即y=﹣ ![]() x2+x+6;
x2+x+6;
(2)
解:设P(m,0),
如图,

∵PE∥AB,
∴△PCE∽△BCA,
∴ ![]() ,
,
![]() ,
,
∴S△PCE= ![]() ,
,
∴S=S△APC﹣S△PCE=﹣ ![]() m2+m+6,
m2+m+6,
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,S有最大值为
时,S有最大值为 ![]() ;
;
∴P( ![]() ,0)
,0)
(3)
解:设平移后的抛物线的顶点为G(h,k),
∴抛物线解析式为y=﹣ ![]() (x﹣h)2+k,
(x﹣h)2+k,
由抛物线的不动点的定义,得,t=﹣ ![]() (t﹣h)2+k,
(t﹣h)2+k,
即:t2+(3﹣2h)t+h2﹣3k=0,
∵平移后,抛物线只有一个不动点,
∴此方程有两个相等的实数根,
∴△=(3﹣2h)2﹣4(h2﹣3k)=0,
∴h﹣k= ![]() ①,
①,
∵顶点在直线y=2x﹣ ![]() 上,
上,
∴k=2k﹣ ![]() ②,
②,
∴联立①②得,h=1,k= ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() =﹣
=﹣ ![]() x2+
x2+ ![]() x﹣
x﹣ ![]()
【解析】(1)已知抛物线与x轴的两个交点坐标,所以设抛物线方程为两点式:y=a(x+3)(x﹣6),然后把点A的坐标代入该函数解析式即可求得系数a的值;(2)利用相似三角形的性质得出S△PCE= ![]() ,进而求出△APE的面积S,即可得出点P坐标;(3)利用抛物线上不动点的定义以及不动点的个数得出方程h﹣k=
,进而求出△APE的面积S,即可得出点P坐标;(3)利用抛物线上不动点的定义以及不动点的个数得出方程h﹣k= ![]() ①,再用平移后的抛物线的顶点在直线y=2x﹣
①,再用平移后的抛物线的顶点在直线y=2x﹣ ![]() 上,得出方程k=2k﹣
上,得出方程k=2k﹣ ![]() ②,联立解方程组即可.
②,联立解方程组即可.
【考点精析】本题主要考查了抛物线与坐标轴的交点和相似三角形的判定的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
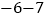 (2)
(2) 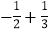
(3)
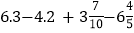 (4)
(4)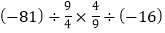
(5)
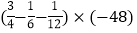 (6)-14+16÷(-2)3×|-3-1|
(6)-14+16÷(-2)3×|-3-1| -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的括号内
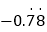 , -
, - , 0,
, 0, 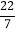 ,‐3.1415926, 20%, ‐3
,‐3.1415926, 20%, ‐3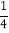 , 2, -1,3.1010010001…(每两个1之间逐次增加1个0)
, 2, -1,3.1010010001…(每两个1之间逐次增加1个0) ①正数集合{ ……}
②负数集合{ ……}
③整数集合{ ……}
④负分数集合{ ……}
⑤无理数集合{ ……}
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1 .
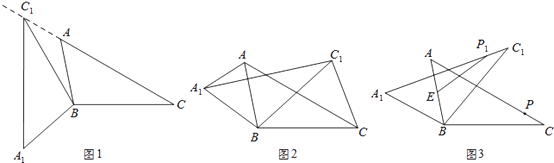
(1)如图1,当点C1在线段CA的延长线时,求∠CC1A1的度数;
(2)已知AB=6,BC=8,
①如图2,连接AA1 , CC1 , 若△CBC1的面积为16,求△ABA1的面积;
②如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应是点P1 , 直接写出线段EP1长度的最大值.
(3)线段EP1长度的最大值为11,理由如下: -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,则反比例函数
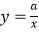 与一次函数y=bx+c在同一坐标系中的大致图象是( )
与一次函数y=bx+c在同一坐标系中的大致图象是( ) 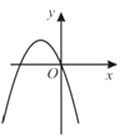
A.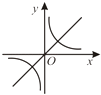
B.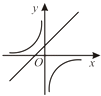
C.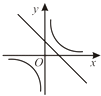
D.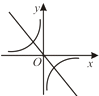
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道:|5|在数轴上表示数5的点与原点的距离,而|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
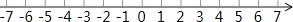
(1)则
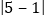 表示 的距离.
表示 的距离.(2)数轴上表示x与 7的两点之间的距离可以表示为 .
(3)如果|x-2|=5,则x= .
(4)同理|x+1|+|x-2|表示数轴上有理数x所对应的点到-1和2所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+1|+|x-2|=3,这样的整数是 .
(5)由以上探索猜想对于任何有理数x,|x+3|+|x-6|的最小值是 .
-
科目: 来源: 题型:
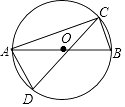
查看答案和解析>>【题目】如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )
A.15°
B.20°
C.25°
D.30°
相关试题

