搜索
【题目】二次函数y=ax2+bx+c的图象如图所示，则反比例函数 
与一次函数y=bx+c在同一坐标系中的大致图象是（ ）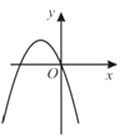 
A.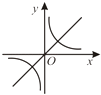
B.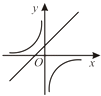
C.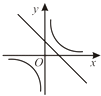
D.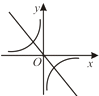
参考答案：
【答案】D
【解析】解：∵二次函数的图象开口向下， ∴反比例函数y= 
的图象必在二、四象限，故A、C错误；
∵二次函数的图象经过原点，
∴c=0，
∴一次函数y=bx+c的图象必经过原点，故B错误．
故选D．
【考点精析】关于本题考查的一次函数的图象和性质和反比例函数的图象，需要了解一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数填在相应的括号内
， -
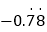, 0,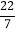 
,‐3.1415926, 20%, ‐3
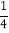, 2, -1，3.1010010001…（每两个1之间逐次增加1个0） ①正数集合{ ……}
②负数集合{ ……}
③整数集合{ ……}
④负分数集合{ ……}
⑤无理数集合{ ……}
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠ACB=30°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1 ．
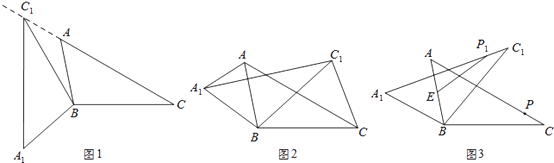
（1）如图1，当点C1在线段CA的延长线时，求∠CC1A1的度数；
（2）已知AB=6，BC=8，
①如图2，连接AA1 ， CC1 ， 若△CBC1的面积为16，求△ABA1的面积；
②如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转的过程中，点P的对应是点P1 ， 直接写出线段EP1长度的最大值．
（3）线段EP1长度的最大值为11，理由如下： -
科目： 来源： 题型：
查看答案和解析>>【题目】将直角边长为6的等腰直角△AOC放在平面直角坐标系中，点O为坐标原点，点C、A分别在x轴，y轴的正半轴上，一条抛物线经过点A、C及点B（﹣3，0）．
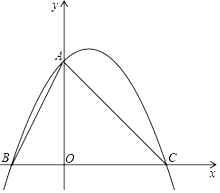
（1）求该抛物线的解析式；
（2）若点P是线段BC上一动点，过点P作AB的平行线交AC于点E，连接AP，当△APE的面积最大时，求点P的坐标；
（3）若点P（t，t）在抛物线上，则称点P为抛物线的不动点，将（1）中的抛物线进行平移，平移后，该抛物线只有一个不动点，且顶点在直线y=2x﹣
上，求此时抛物线的解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】同学们都知道：|5|在数轴上表示数5的点与原点的距离，而|5-（-2）|表示5与-2之差的绝对值，实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离．请你借助数轴进行以下探索：
（1）则
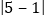表示 的距离．（2）数轴上表示x与 7的两点之间的距离可以表示为 .
（3）如果|x-2|=5，则x= .
（4）同理|x+1|+|x-2|表示数轴上有理数x所对应的点到-1和2所对应的点的距离之和，请你找出所有符合条件的整数x，使得|x+1|+|x-2|=3，这样的整数是 .
（5）由以上探索猜想对于任何有理数x，|x+3|+|x-6|的最小值是 .
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，C，D是以线段AB为直径的⊙O上两点，若CA=CD，且∠ACD=30°，则∠CAB=（ ）
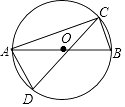
A.15°
B.20°
C.25°
D.30° -
科目： 来源： 题型：
【题目】随着手机的普及，微信
一种聊天软件
的兴起，许多人抓住这种机会，做起了“微商”，很多农产品也改变了原来的销售模式，实行了网上销售，这不刚大学毕业的小明把自家的冬枣产品也放到了网上，他原计划每天卖100斤冬枣，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某周的销售情况超额记为正，不足记为负
单位：斤；星期
一
二
三
四
五
六
日
与计划量的差值
(1)根据记录的数据可知前三天共卖出 ______ 斤；
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤；
(3)本周实际销售总量达到了计划数量没有？
(4)若冬季每斤按8元出售，每斤冬枣的运费平均3元，那么小明本周一共收入多少元？ 查看答案和解析>>
相关试题
