【题目】如图,已知反比例函数![]() 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
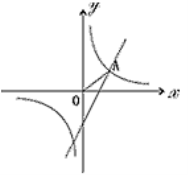
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上, 求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由。
参考答案:
【答案】(1)y=![]() ;(2)(1,1);(3)符合条件的点有4个,分别是(
;(2)(1,1);(3)符合条件的点有4个,分别是(![]() ,0),(-
,0),(-![]() ,0),(2,0),(1,0).
,0),(2,0),(1,0).
【解析】
试题分析:(1)把过一次函数的两个点代入一次函数,即可求得k,进而求得反比例函数的解析式;(2)同时在这两个函数解析式上,让这两个函数组成方程组求解即可;(3)应先求出OA的距离,然后根据:OA=OP,OA=AP,OP=AP,分情况讨论解决.
试题解析:(1)由题意得 ![]() ,②-①得:k=2,∴反比例函数的解析式为y=
,②-①得:k=2,∴反比例函数的解析式为y=![]() ;
;
(2)由 ,解得
,解得![]() ,
,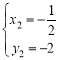 ,∵点A在第一象限,∴点A的坐标为(1,1);
,∵点A在第一象限,∴点A的坐标为(1,1);
(3)OA=![]() =
=![]() ,OA与x轴所夹锐角为45°,①当OA为腰时,由OA=
,OA与x轴所夹锐角为45°,①当OA为腰时,由OA=![]() 得
得![]() (
(![]() ,0),由OA=
,0),由OA=![]() 得
得![]() (-
(-![]() ,0);由OA=
,0);由OA=![]() 得
得![]() (2,0).②当OA为底时,
(2,0).②当OA为底时,![]() =
=![]() 得
得![]() (1,0).
(1,0).
∴符合条件的点有4个,分别是(![]() ,0),(-
,0),(-![]() ,0),(2,0),(1,0).
,0),(2,0),(1,0).

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点A表示,小红家用点B表示,小刚家用点C表示)

(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
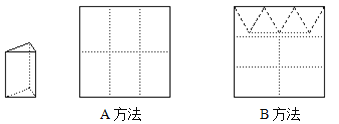
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数
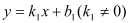 的图象为直线
的图象为直线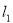 ,一次函数
,一次函数 的图象为直线
的图象为直线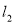 ,若
,若 ,且
,且 ,我们就称直线
,我们就称直线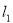 与直线
与直线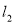 互相平行.已知一次函数
互相平行.已知一次函数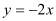 的图象为直线
的图象为直线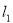 ,过点
,过点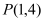 且与已知直线
且与已知直线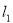 平行的直线为
平行的直线为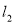 。
。解答下面的问题:
(1)求
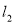 的函数表达式;
的函数表达式;(2)设直线
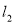 分别与
分别与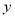 轴、
轴、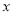 轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求
轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求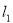 和
和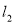 两平行线之间的距离 ;
两平行线之间的距离 ;(3)若Q为OA上一动点,求QP+QB的最小值,并求取得最小值时Q点的坐标。
(4)在
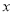 轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,等边△ABC内接于⊙O,点P是劣弧
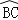 上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
上的一点(端点除外),延长BP至D,使BD=AP,连接CD.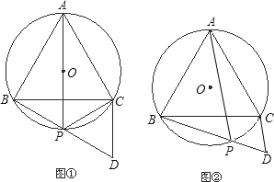
(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;
(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
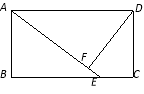
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
相关试题

