【题目】如图,点A为函数y= ![]() (x>0)图象上一点,连结OA,交函数y=
(x>0)图象上一点,连结OA,交函数y= ![]() (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 . 
参考答案:
【答案】6
【解析】解:设点A的坐标为(a, ![]() ),点B的坐标为(b,
),点B的坐标为(b, ![]() ),
),
∵点C是x轴上一点,且AO=AC,
∴点C的坐标是(2a,0),
设过点O(0,0),A(a, ![]() )的直线的解析式为:y=kx,∴
)的直线的解析式为:y=kx,∴ ![]() ,解得,k=
,解得,k= ![]() ,
,
又∵点B(b, ![]() )在y=
)在y= ![]() 上,
上,
∴ ![]() ,解得,
,解得, ![]() 或
或 ![]() (舍去),
(舍去),
∴S△ABC=S△AOC﹣S△OBC= ![]() =
= ![]() ,
,
所以答案是:6.
【考点精析】掌握反比例函数的图象和三角形的面积是解答本题的根本,需要知道反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;三角形的面积=1/2×底×高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点
 ,点
,点 第一次跳动至带你
第一次跳动至带你 ,第二次点
,第二次点 跳动至带你
跳动至带你 ,第三次点
,第三次点 跳动至带你
跳动至带你 ,第四次点
,第四次点 跳动至带你
跳动至带你 ,…… 依此规律跳动下去,则点
,…… 依此规律跳动下去,则点 与点
与点 之间的距离是( )
之间的距离是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为m(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=
 ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:

(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
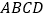 是矩形,点
是矩形,点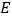 在线段
在线段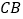 的延长线上,连接
的延长线上,连接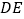 交
交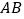 于点
于点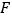 ,
,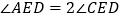 ,点
,点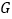 是
是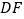 的中点.
的中点.(
 )求证:
)求证: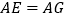 .
.(
 )若
)若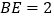 ,
,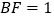 ,
,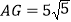 ,点
,点 是
是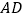 的中点,求
的中点,求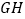 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的对角线AC,BD交于点O,点E,F分别是OB,OC上的动点.当动点E,F满足BE=CF时.
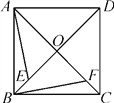
(1)写出所有以点E或F为顶点的全等三角形;(不得添加辅助线)
(2)求证:AE⊥BF.
相关试题

