【题目】如图,已知正方形ABCD的对角线AC,BD交于点O,点E,F分别是OB,OC上的动点.当动点E,F满足BE=CF时.
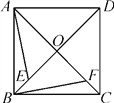
(1)写出所有以点E或F为顶点的全等三角形;(不得添加辅助线)
(2)求证:AE⊥BF.
参考答案:
【答案】(1) △ABE≌△BCF,△AOE≌△BOF,△ADE≌△BAF;(2)见解析
【解析】试题分析:
(1)由已知条件易得AB=BC,∠ABE=∠CBF=45°,结合BE=CF可得△ABE≌△BCF;由此可得∠AEB=∠CFB,从而可得∠AEO=∠BFO,结合∠AOE=∠BOF=90°及OA=OB可得△AOE≌△BOF;由∠ADE=∠BAF=45°,∠AED=∠BFA结合AD=AB即可得到△ADE≌△BAF;
(2)延长AE交BF于点M,由△ABE≌△BCF,可得∠BAE=∠CBF,结合∠CBF+∠ABF=90°可得∠BAE+∠ABM=90°,从而可得∠AMB=90°,由此即可得到AE⊥BF.
试题解析:
(1)由题意可得:
图中以点E或F为顶点的全等三角形有:△ABE≌△BCF,△AOE≌△BOF,△ADE≌△BAF;
(2)延长AE交BF于点M,
∵△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠CBF+∠ABF=90°,
∴∠BAE+∠ABF=90°,
∴∠AMB=90°,
∴AE⊥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A为函数y=
 (x>0)图象上一点,连结OA,交函数y=
(x>0)图象上一点,连结OA,交函数y=  (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 .
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:

(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是矩形,点
是矩形,点 在线段
在线段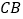 的延长线上,连接
的延长线上,连接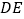 交
交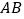 于点
于点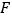 ,
,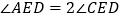 ,点
,点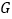 是
是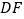 的中点.
的中点.(
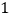 )求证:
)求证: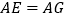 .
.(
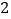 )若
)若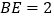 ,
,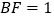 ,
,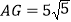 ,点
,点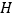 是
是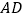 的中点,求
的中点,求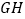 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 .试说明
.试说明 ∥
∥ ,请完成下列填空,把证明过程补充完整.
,请完成下列填空,把证明过程补充完整.证明: ∵ __________________________ ,
∴
 (_________________).
(_________________).∴

又∵

∴ __________________ (_____________________),
∴
 ∥
∥ (_______________________________).
(_______________________________). 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
 三点的坐标分别为
三点的坐标分别为 .
.(1)画出三角形
 ,并求三角形
,并求三角形 的面积;
的面积;(2)如图,三角形
 可以由三角形
可以由三角形 向右平移 _____ 个单位,然后向下平移 _____ 个单位得到;若点
向右平移 _____ 个单位,然后向下平移 _____ 个单位得到;若点 为三角形
为三角形 内一点,则点
内一点,则点 在三角形
在三角形 内的对应点
内的对应点 的坐标为 _________ .
的坐标为 _________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】国民体质监测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况.我们队专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:


(1)在这次形体测评中,一共抽查了多少名学生?如果全市约有10万名初中生,那么全市初中生中三姿不良的学生约有多少人?
(2)请直接将两幅图补充完整.
相关试题

