【题目】如图,在平面直角坐标系xOy中,已知直线AB:y= ![]() x+4交x轴于点A,交y轴于点B.直线CD:y=﹣
x+4交x轴于点A,交y轴于点B.直线CD:y=﹣ ![]() x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.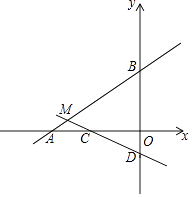
(1)直接写出点B和点D的坐标;
(2)若点P是射线MD上的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B、E、P、M为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点E的坐标;若不存在,说明理由.
参考答案:
【答案】
(1)解:∵点B是直线AB:y= ![]() x+4与y轴的交点坐标,
x+4与y轴的交点坐标,
∴B(0,4),
∵点D是直线CD:y=﹣ ![]() x﹣1与y轴的交点坐标,
x﹣1与y轴的交点坐标,
∴D(0,﹣1);
(2)解:如图1,∵直线AB与CD相交于M,
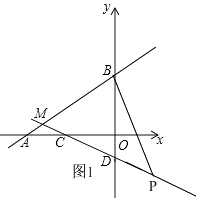
∴M(﹣5, ![]() ),
),
∵点P的横坐标为x,
∴点P(x,﹣ ![]() x﹣1),
x﹣1),
∵B(0,4),D(0,﹣1),
∴BD=5,
∵点P在射线MD上,即:x≥0时,
S=S△BDM+S△BDP= ![]() ×5(5+x)=
×5(5+x)= ![]() x+
x+ ![]() ,
,
(3)解:如图,由(1)知,S= ![]() x+
x+ ![]() ,
,
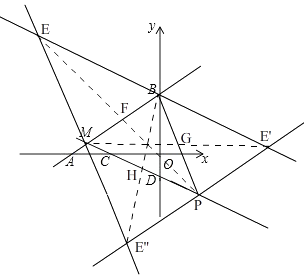
当S=20时, ![]() x+
x+ ![]() =20,
=20,
∴x=3,
∴P(3,﹣2),
①当BP是对角线时,取BP的中点G,连接MG并延长取一点E'使GE'=GE,
设E'(m,n),
∵B(0,4),P(3,﹣2),
∴BP的中点坐标为( ![]() ,1),
,1),
∵M(﹣5, ![]() ),
),
∴ ![]() =
= ![]() ,
, ![]() =1,
=1,
∴m=8,n= ![]() ,
,
∴E'(8, ![]() ),
),
②当AB为对角线时,同①的方法得,E(﹣9,6),
③当MP为对角线时,同①的方法得,E'(﹣2,﹣ ![]() ),
),
即:满足条件的点E的坐标为(8, ![]() )、(﹣9,6)、(﹣2,﹣
)、(﹣9,6)、(﹣2,﹣ ![]() ).
).
【解析】(1)将x=0代入函数解析式得到对应的y值,从而可得到点B和点D的坐标;
(2)将所求三角形的面积转为△BDM和△BDP的面积之和,然后依据三角形的面积公式列出函数关系式即可;
(3)分三种情况利用对角线互相平分的四边形是平行四边形和线段的中点坐标的确定方法即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各点中,在x 轴上的是( ).
A. (3,-3)B. (0,3)C. (-3,0)D. (3,-4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(-3,-2019)在:( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km
),甲车行驶的时间为x(h),y甲 , y乙与x之间的函数图象如图所示,结合图象解答下列问题: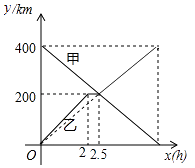
(1)当0<x<2时,求乙车的速度;
(2)求乙车与甲车相遇后y乙与x的关系式;
(3)当两车相距20km时,直接写出x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,则菱形ABCD的面积是( )
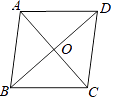
A.24
B.26
C.30
D.48 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初三(1)班的一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男、女生的人数之比为( )
A.1:2
B.2:1
C.3:2
D.2:3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面上四点A(0,0),B(10,0),C(12,6),D(2,6),直线y=mx﹣3m+6将四边形ABCD分成面积相等的两部分,则m的值为( )
A.
B.﹣1
C.2
D.
相关试题

