【题目】已知平面上四点A(0,0),B(10,0),C(12,6),D(2,6),直线y=mx﹣3m+6将四边形ABCD分成面积相等的两部分,则m的值为( )
A.![]()
B.﹣1
C.2
D.![]()
参考答案:
【答案】B
【解析】解:如图,∵A(0,0),B(10,0),C(12,6),D(2,6),
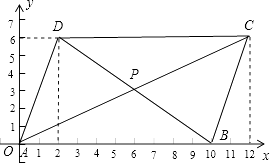
∴AB=10﹣0=10,CD=12﹣2=10,
又点C、D的纵坐标相同,
∴AB∥CD且AB=CD,
∴四边形ABCD是平行四边形,
∵12÷2=6,6÷2=3,
∴对角线交点P的坐标是(6,3),
∵直线y=mx﹣3m+6将四边形ABCD分成面积相等的两部分,
∴直线y=mx﹣3m+6经过点P,
∴6m﹣3m+6=3,
解得m=﹣1.
所以答案是:B.
【考点精析】掌握确定一次函数的表达式是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知直线AB:y=
 x+4交x轴于点A,交y轴于点B.直线CD:y=﹣
x+4交x轴于点A,交y轴于点B.直线CD:y=﹣  x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.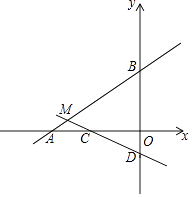
(1)直接写出点B和点D的坐标;
(2)若点P是射线MD上的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B、E、P、M为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点E的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,则菱形ABCD的面积是( )
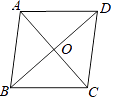
A.24
B.26
C.30
D.48 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初三(1)班的一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男、女生的人数之比为( )
A.1:2
B.2:1
C.3:2
D.2:3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠A=90°,DE∥BC,F,G,H,I分别是DE,BE,BC,CD的中点,连接FG,GH,HI,IF,FH,GI.对于下列结论:①∠GFI=90°;②GH=GI;③GI=
 (BC﹣DE);④四边形FGHI是正方形.其中正确的是(请写出所有正确结论的序号).
(BC﹣DE);④四边形FGHI是正方形.其中正确的是(请写出所有正确结论的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点(-4,5)到x轴上的距离是_______,到y轴上的距离是_______。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平行四边形ABCD中,AC交BD于点O,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:四边形AECF为平行四边形.
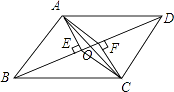
相关试题

