【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km
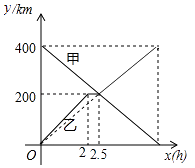
),甲车行驶的时间为x(h),y甲 , y乙与x之间的函数图象如图所示,结合图象解答下列问题: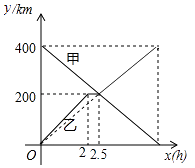
(1)当0<x<2时,求乙车的速度;
(2)求乙车与甲车相遇后y乙与x的关系式;
(3)当两车相距20km时,直接写出x的值.
参考答案:
【答案】
(1)解:200÷2=100(km/h).
答:当0<x<2时,乙车的速度为100km/h.
(2)解:甲车的速度为(400﹣200)÷2.5=80(km/h),
甲、乙两车到达目的地的时间为400÷80=5(h).
设乙车与甲车相遇后y乙与x的关系式为y乙=kx+b,
将点(2.5,200)、(5,400)代入y乙=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴乙车与甲车相遇后y乙与x的关系式为y乙=80x(2.5≤x≤5).
(3)解:根据题意得:y乙= 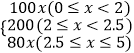 ,
,
y甲=400﹣80x(0≤x≤5).
当0≤x<2时,400﹣80x﹣100x=20,
解得:x= ![]() >2(不合题意,舍去);
>2(不合题意,舍去);
当2≤x<2.5时,400﹣80x﹣200=20,
解得:x= ![]() ;
;
当2.5≤x≤5时,80x﹣(400﹣80x)=20,
解得:x= ![]() .
.
综上所述:当x的值为 ![]() 或
或 ![]() 时,两车相距20km.
时,两车相距20km.
【解析】(1)先根据函数图像确定乙车行驶2小时所行驶的路程,然后再根据速度=路程÷时间求解即可;
(2)依据函数图像可得到甲车行驶2.5行驶的路程,然后根据速度=路程÷时间可求出甲车的速度,由时间=路程÷速度可求出甲、乙两车到达目的地的时间,再结合二者相遇的时间,利用待定系数法即可求出乙车与甲车相遇后y乙与x的关系式;
(3)根据数量关系,找出y甲、y乙关于x的函数关系式,分0≤x<2、2≤x<2.5和2.5≤x≤5三种情况,列出关于x的一元一次方程,最后解关于x的一元一次方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的四个内角∠A、∠B、∠C、∠D度数之比依次如下,那么其中是平行四边形的是( )。
A. 1:2:3:4 B. 2:3:2:3 C. 2:3:3:2 D. 1:3:3:2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各点中,在x 轴上的是( ).
A. (3,-3)B. (0,3)C. (-3,0)D. (3,-4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(-3,-2019)在:( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知直线AB:y=
 x+4交x轴于点A,交y轴于点B.直线CD:y=﹣
x+4交x轴于点A,交y轴于点B.直线CD:y=﹣  x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.
x﹣1与直线AB相交于点M,交x轴于点C,交y轴于点D.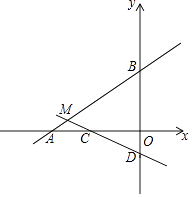
(1)直接写出点B和点D的坐标;
(2)若点P是射线MD上的一个动点,设点P的横坐标是x,△PBM的面积是S,求S与x之间的函数关系;
(3)当S=20时,平面直角坐标系内是否存在点E,使以点B、E、P、M为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点E的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,则菱形ABCD的面积是( )
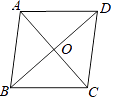
A.24
B.26
C.30
D.48 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初三(1)班的一次数学测试的平均成绩为80分,男生平均成绩为82分,女生平均成绩为77分,则该班男、女生的人数之比为( )
A.1:2
B.2:1
C.3:2
D.2:3
相关试题

