【题目】2015年12月16日,南京大报恩寺遗址公园正式对外开放.某校数学兴趣小组想测量大报恩塔的高度.如图,成员小明利用测角仪在B处测得塔顶的仰角α=63.5°,然后沿着正对该塔的方向前进了13.1m到达E处,再次测得塔顶的仰角β=71.6°.测角仪BD的高度为1.4m,那么该塔AC的高度是多少?(参考数据:sin63.5°≈0.90,cos63.5°≈0.45,tan63.5°≈2.00,sin71.6°≈0.95,cos71.6°≈0.30,tan71.6°≈3.00)


参考答案:
【答案】该塔AC的高度约80m.
【解析】分析:延长DF交AC于点G,设AG=xm,根据正切的概念用x表示出DG和FG,根据图形列出方程求出x的值,计算即可.
详解:延长DF交AC于点G,
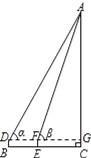
设AG=xm.由题意知:DF=13.1 m,DB=FE=GC=1.4 m.
在Rt△ADG中,tan∠ADG=![]() ,∴DG=
,∴DG=![]() =
=![]() ≈
≈![]() ,
,
在Rt△AFG中,tan∠AFG=![]() ,∴FG=
,∴FG=![]() =
=![]() ≈
≈![]() ,
,
∵DF=DG﹣FG,∴![]() =13.1,解得x=78.6,∴AG=78.6 m,
=13.1,解得x=78.6,∴AG=78.6 m,
∵AC=AG+GC,∴AC=78.6+1.4=80(m).
答:该塔AC的高度约80m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
-
科目: 来源: 题型:
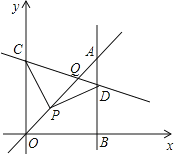
查看答案和解析>>【题目】如图,点C为y轴正半轴上一点,点P(2,2)在直线y=x上,PD=PC,且PD⊥PC,过点D作直线AB⊥x轴于B,直线AB与直线y=x交于点A,直线CD与直线y=x交于点Q,当∠CPA=∠PDB时,则点Q的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校与图书馆在冋一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达日的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
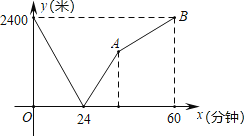
(1)根据图象信息,当t= 分钟时甲乙两人相遇,乙的速度为 米/分钟;
(2)求点A的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)以下四边形中,是勾股四边形的为 .(填写序号即可)
①矩形;②有一个角为直角的任意凸四边形;③有一个角为60°的菱形.
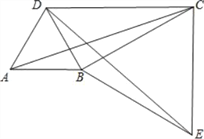
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,∠DCB=30°,连接AD,DC,CE.
①求证:△BCE是等边三角形;
②求证:四边形ABCD是勾股四边形.
-
科目: 来源: 题型:
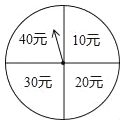
查看答案和解析>>【题目】端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得 元购物券,最多可得 元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
相关试题

