【题目】甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
参考答案:
【答案】(1)![]() .
.
(2)![]() .
.
(3)甲先摸出“锤子”获胜的可能性最大.
【解析】
(1)当问题情境是从若干个元素中抽取一个元素(即一次性操作问题)时,可以直接应用公式![]() (m表示事件A发生可能出现的结果数,n表示一次实验中所有等可能出现的结果数);(2)因为甲先摸出了“石头”后无放回,所以袋子中还有14张卡片;(3)甲先摸,摸到“锤子”、“石头”、“剪子”、“布”的可能性都有,所以要分类讨论.
(m表示事件A发生可能出现的结果数,n表示一次实验中所有等可能出现的结果数);(2)因为甲先摸出了“石头”后无放回,所以袋子中还有14张卡片;(3)甲先摸,摸到“锤子”、“石头”、“剪子”、“布”的可能性都有,所以要分类讨论.
(1)若甲先摸,共有15张卡片可供选择,其中写有“石头”的卡片共3张,
故甲摸出“石头”的概率为![]() .
.
(2)若甲先摸且摸出“石头”,则可供乙选择的卡片还有14张,其中乙只有摸出卡片“锤子”或“布”才能获胜,这样的卡片共有8张,故乙获胜的概率为![]() .
.
(3)若甲先摸,则“锤子”、“石头”、“剪子”、“布”四种卡片都有可能被摸出.
若甲先摸出“锤子”,则甲获胜(即乙摸出“石头”或“剪子”)的概率为![]() ;
;
若甲先摸出“石头”,则甲获胜(即乙摸出“剪子”)的概率为![]() ;
;
若甲先摸出“剪子”,则甲获胜(即乙摸出“布”)的概率为![]() ;
;
若甲先摸出“布”,则甲获胜(即乙摸出“锤子”或“石头”)的概率为![]() .
.
故甲先摸出“锤子”获胜的可能性最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某地,人们发现某种蟋蟀1min,所叫次数x与当地温度T之间的关系或为T=ax+b,下面是蟋蟀所叫次数与温度变化情况对照表:
蟋蟀叫的次数(x)
…
84
98
119
…
温度(℃)T
…
15
17
20
…
①根据表中的数据确定a、b的值.
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时掷两个质地均匀的骰子,观察向上一面的点数,两个骰子的点数相同的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩
划记
频数
百分比
优秀
正正正
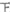
a
30%
良好
正正正正正正
30
b
合格
正
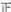
9
15%
不合格
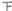
3
5%
合计
60
60
100%
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a=_____,b=_____;
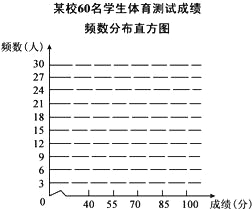
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为y轴正半轴上一点,点P(2,2)在直线y=x上,PD=PC,且PD⊥PC,过点D作直线AB⊥x轴于B,直线AB与直线y=x交于点A,直线CD与直线y=x交于点Q,当∠CPA=∠PDB时,则点Q的坐标是_____.
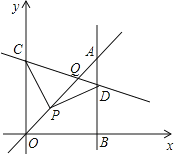
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校与图书馆在冋一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达日的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
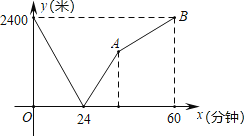
(1)根据图象信息,当t= 分钟时甲乙两人相遇,乙的速度为 米/分钟;
(2)求点A的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年12月16日,南京大报恩寺遗址公园正式对外开放.某校数学兴趣小组想测量大报恩塔的高度.如图,成员小明利用测角仪在B处测得塔顶的仰角α=63.5°,然后沿着正对该塔的方向前进了13.1m到达E处,再次测得塔顶的仰角β=71.6°.测角仪BD的高度为1.4m,那么该塔AC的高度是多少?(参考数据:sin63.5°≈0.90,cos63.5°≈0.45,tan63.5°≈2.00,sin71.6°≈0.95,cos71.6°≈0.30,tan71.6°≈3.00)


相关试题

