【题目】如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G. 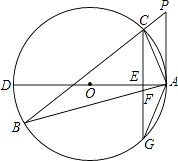
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AFAB;
(3)若⊙O的直径为10,AC=2 ![]() ,AB=4
,AB=4 ![]() ,求△AFG的面积.
,求△AFG的面积.
参考答案:
【答案】
(1)解:PA与⊙O相切.理由:
连接CD,

∵AD为⊙O的直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
∵∠B=∠D,∠PAC=∠B,
∴∠PAC=∠D,
∴∠PAC+∠CAD=90°,
即DA⊥PA,
∵点A在圆上,
∴PA与⊙O相切
(2)解:证明:如图2,连接BG,
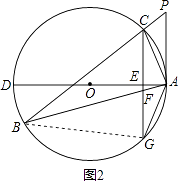
∵AD为⊙O的直径,CG⊥AD,
∴ ![]() =
= ![]() ,
,
∴∠AGF=∠ABG,
∵∠GAF=∠BAG,
∴△AGF∽△ABG,
∴AG:AB=AF:AG,
∴AG2=AFAB
(3)解:解:如图3,连接BD,
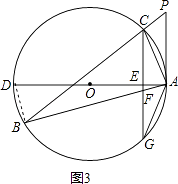
∵AD是直径,
∴∠ABD=90°,
∵AG2=AFAB,AG=AC=2 ![]() ,AB=4
,AB=4 ![]() ,
,
∴AF= ![]() =
= ![]() ,
,
∵CG⊥AD,
∴∠AEF=∠ABD=90°,
∵∠EAF=∠BAD,
∴△AEF∽△ABD,
∴ ![]() ,
,
即 ![]() ,
,
解得:AE=2,
∴EF= ![]() =1,
=1,
∵EG= ![]() =4,
=4,
∴FG=EG﹣EF=4﹣1=3,
∴S△AFG= ![]() FGAE=
FGAE= ![]() ×3×2=3.
×3×2=3.
【解析】(1)首先连接CD,由AD为⊙O的直径,可得∠ACD=90°,然后由圆周角定理,证得∠B=∠D,由已知∠PAC=∠B,可证得DA⊥PA,继而可证得PA与⊙O相切.(2)首先连接BG,易证得△AFG∽△AGB,然后由相似三角形的对应边成比例,证得结论;(3)首先连接BD,由AG2=AFAB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.

(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: ≈1.414,
≈1.414,  ≈1.732)
≈1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进某种茶壶、茶杯共200个进行销售,其中茶杯的数量是茶壶数量的5倍还多20个.销售方式有两种:(1)单个销售;(2)成套销售.相关信息如下表:
进价(元/个)
单个售价(元/个)
成套售价(元/套)
茶壶
24
a
55
茶杯
4
a﹣30
备注:(1)一个茶壶和和四个茶杯配成一套(如图);
(2)利润=(售价﹣进价)×数量
(1)该商店购进茶壶和茶杯各有多少个?
(2)已知甲顾客花180元购买的茶壶数量与乙顾客花30元购买的茶杯数量相同.
①求表中a的值.
②当该商店还剩下20个茶壶和100个茶杯时,商店将这些茶壶和茶杯中的一部分按成套销售,其余按单个销售,这120个茶壶和茶杯全部售出后所得的利润为365元.问成套销售了多少套?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m、n满足等式
 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线
 、
、 、
、 上,且
上,且 ,
, ,之间的距离为2 ,
,之间的距离为2 ,  ,
, 之间的距离为3 ,则AC2= _______.
之间的距离为3 ,则AC2= _______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.

(1)直接写出抛物线的解析式:;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.
相关试题

