【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,之间的距离为2 ,
,之间的距离为2 , ![]() ,
,![]() 之间的距离为3 ,则AC2= _______.
之间的距离为3 ,则AC2= _______.

参考答案:
【答案】68
【解析】
过A、C点作l3的垂线构造出直角三角形,根据三角形全等求出BE=AD=3,再由勾股定理求出BC的长,再利用勾股定理即可求出AC的长,最后得到AC2.
作AD⊥l3于D,作CE⊥l3于E,
∵∠ABC=90°,∴∠ABD+∠CBE=90°,
又∠DAB+∠ ABD=90°,
∴∠BAD=∠CBE,
在△ABD和△BEC中,
 ,
,
∴△ABD≌△BCE (AAS),
,∴BE=AD=3,
在Rt△BCE中,根据勾股定理,得![]() ,
,
在Rt△ABC中,根据勾股定理,得![]() .故答案是68.
.故答案是68.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.
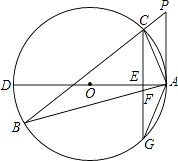
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AFAB;
(3)若⊙O的直径为10,AC=2 ,AB=4
,AB=4  ,求△AFG的面积.
,求△AFG的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m、n满足等式
 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.

(1)直接写出抛物线的解析式:;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,对角线AC、BD交于点O,过点O作直线EF分别交线段AD、BC于点E、F.
(1)根据题意,画出图形,并标上正确的字母;
(2)求证:DE=BF. -
科目: 来源: 题型:
查看答案和解析>>【题目】初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如图的统计图:

(1)这次调查的家长总人数为人,表示“无所谓”的家长人数为人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是;
(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.
相关试题

