【题目】如图,已知抛物线y=ax2+bx+4与x轴交于A(﹣2,0)、B两点,与y轴交于C点,其对称轴为直线x=1.
(1)直接写出抛物线的解析式:;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形?若存在,求出E、F的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)y=﹣ ![]() x2+x+4
x2+x+4
(2)
解:由抛物线y=﹣ ![]() x2+x+4可知C(0,4),
x2+x+4可知C(0,4),
∵抛物线的对称轴为直线x=1,根据对称性,
∴C′(2,4),
∴A′(0,0)
(3)
解:存在.
设F(x,﹣ ![]() x2+x+4).
x2+x+4).
以A、C、E、F为顶点的四边形为平行四边形,
①若AC为平行四边形的边,如答图1﹣1所示,则EF∥AC且EF=AC.
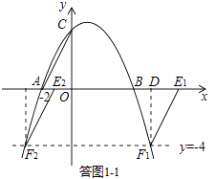
过点F1作F1D⊥x轴于点D,则易证Rt△AOC≌Rt△E1DF1,
∴DE1=2,DF1=4.
∴﹣ ![]() x2+x+4=﹣4,
x2+x+4=﹣4,
解得:x1=1+ ![]() ,x2=1﹣
,x2=1﹣ ![]() .
.
∴F1(1+ ![]() ,﹣4),F2(1﹣
,﹣4),F2(1﹣ ![]() ,﹣4);
,﹣4);
∴E1(3+ ![]() ,0),E2(3﹣
,0),E2(3﹣ ![]() ,0).
,0).
②若AC为平行四边形的对角线,如答图1﹣2所示.
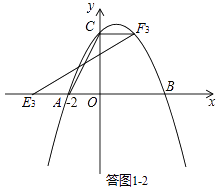
∵点E3在x轴上,∴CF3∥x轴,
∴点C为点A关于x=1的对称点,
∴F3(2,4),CF3=2.
∴AE3=2,
∴E3(﹣4,0),
综上所述,存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形;
点E、F的坐标为:E1(3+ ![]() ,0),F1(1+
,0),F1(1+ ![]() ,﹣4);E2(3﹣
,﹣4);E2(3﹣ ![]() ,0),F2(1﹣
,0),F2(1﹣ ![]() ,﹣4);E3(﹣4,0),F3(2,4)
,﹣4);E3(﹣4,0),F3(2,4)
【解析】解:(1)∵A(﹣2,0),对称轴为直线x=1.
∴B(4,0),
把A(﹣2,0),B(4,0)代入抛物线的表达式为:![]() ,
,
解得: 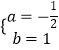 ,
,
∴抛物线的解析式为:y=﹣ ![]() x2+x+4;
x2+x+4;
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为⊙O的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD交AD于E,交AB于F,交⊙O于G.
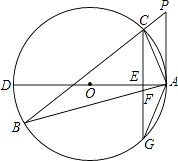
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AFAB;
(3)若⊙O的直径为10,AC=2 ,AB=4
,AB=4  ,求△AFG的面积.
,求△AFG的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m、n满足等式
 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______.
,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线
 、
、 、
、 上,且
上,且 ,
, ,之间的距离为2 ,
,之间的距离为2 ,  ,
, 之间的距离为3 ,则AC2= _______.
之间的距离为3 ,则AC2= _______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,对角线AC、BD交于点O,过点O作直线EF分别交线段AD、BC于点E、F.
(1)根据题意,画出图形,并标上正确的字母;
(2)求证:DE=BF. -
科目: 来源: 题型:
查看答案和解析>>【题目】初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“初中学生带手机上学”现象的看法,统计整理并制作了如图的统计图:

(1)这次调查的家长总人数为人,表示“无所谓”的家长人数为人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是;
(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米的A点处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.

(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间.(参考数据: ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
相关试题

