【题目】乘法公式的探究及应用.
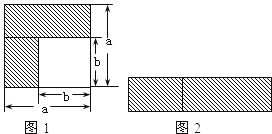
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
参考答案:
【答案】(1)a2﹣b2(2)a﹣b,a+b,(a+b)(a﹣b)(3)99.96(4)①99.96②4m2﹣n2+2np﹣p2
【解析】
试题分析:(1)利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便简单的计算.
解:(1)利用正方形的面积公式可知:阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;
(2)由图可知矩形的宽是a﹣b,长是a+b,所以面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);
(3)(a+b)(a﹣b)=a2﹣b2(等式两边交换位置也可);
故答案为:(a+b)(a﹣b)=a2﹣b2;
(4)①解:原式=(10+0.2)×(10﹣0.2),
=102﹣0.22,
=100﹣0.04,
=99.96;
②解:原式=[2m+(n﹣p)]×[2m﹣(n﹣p)],
=(2m)2﹣(n﹣p)2,
=4m2﹣n2+2np﹣p2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: ①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )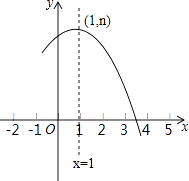
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校改造一个边长为
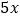 米的正方形花坛,经规划后,南北向要缩短
米的正方形花坛,经规划后,南北向要缩短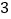 米,东西向要加长
米,东西向要加长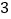 米,则改造后花坛的面积是________平方米,改造后花坛的面积减少了________平方米.
米,则改造后花坛的面积是________平方米,改造后花坛的面积减少了________平方米. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.例如:
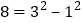 ,
,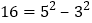 ,
,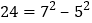 ;则
;则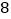 、
、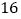 、
、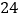 这三个数都是奇特数.
这三个数都是奇特数. (1)
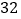 和
和 这两个数是奇特数吗?若是,表示成两个连续奇数的平方差形式.
这两个数是奇特数吗?若是,表示成两个连续奇数的平方差形式.(2)设两个连续奇数是
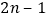 和
和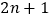 (其中
(其中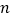 取正整数),由这两个连续奇数构造的奇特数是
取正整数),由这两个连续奇数构造的奇特数是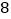 的倍数吗?为什么?
的倍数吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=4,点P是BC边上的动点,点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.
x
…
﹣1
0
1
2
3
…
y
…
b
1
0
1
2
…
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .

相关试题

