【题目】如图,在等边△ABC中,AB=4,点P是BC边上的动点,点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是 . 
参考答案:
【答案】6≤MN≤4 ![]()
【解析】解:(解法一)如图1,当点P为BC的中点时,MN最短. 此时E、F分别为AB、AC的中点,
∴PE= ![]() AC,PF=
AC,PF= ![]() AB,EF=
AB,EF= ![]() BC,
BC,
∴MN=ME+EF+FN=PE+EF+PF=6;
如图2,当点P和点B(或点C)重合时,此时BN(或CM)最长.
此时G(H)为AB(AC)的中点,
∴CG=2 ![]() (BH=2
(BH=2 ![]() ),
),
CM=4 ![]() (BN=4
(BN=4 ![]() ).
).
故线段MN长的取值范围是6≤MN≤4 ![]() .
.
故答案为:6≤MN≤4 ![]() .
.
(解法二)连接PM交AB于点E,连接PN交AC于点F,过点M作MD⊥PN于点D,如图3所示.
设BP=x(0≤x≤4),则PE= ![]() x,CP=4﹣x,PF=
x,CP=4﹣x,PF= ![]() (4﹣x),
(4﹣x),
∴PM= ![]() x,PN=
x,PN= ![]() (4﹣x).
(4﹣x).
∵∠B=∠C=60°,
∴∠BPE=∠CPF=30°,
∴∠MPD=∠BPE+∠BPD=∠BPE+∠CPF=60°,
∴DP= ![]() PM=
PM= ![]() x,MD=
x,MD= ![]() PM=
PM= ![]() x.
x.
在Rt△MDN中,MD= ![]() x,ND=PN+PD=
x,ND=PN+PD= ![]() (4﹣x)+
(4﹣x)+ ![]() x=
x= ![]() (8﹣x),
(8﹣x),
∴MN2=MD2+ND2=3(x﹣2)2+36,
∴当x=2时,MN取最小值6;当x=0或x=4时,MN取最大值4 ![]() .
.
故答案为:6≤MN≤4 ![]() .
.
(解法三)连接AM、AN、AP,过点A作AD⊥MN于点D,如图所示.
∵点P关于直线AB,AC的对称点分别为M,N,
∴AM=AP=AN,∠MAB=∠PAB,∠NAC=∠PAC,
∴△MAN为顶角为120°的等腰三角形,
∴∠AMD=30°,
∴AD= ![]() AM,MD=
AM,MD= ![]() AM,MN=
AM,MN= ![]() AM.
AM.
∵AM=AP,2 ![]() ≤AP≤4,
≤AP≤4,
∴6≤MN≤4 ![]() .
.
故答案为:6≤MN≤4 ![]() .
.

(方法一)当点P为BC的中点时,MN最短,求出此时MN的长度,当点P与点B(或C)重合时,BN(或CM)最长,求出此时BN(或CM)的长度,由此即可得出MN的取值范围.
(方法二)连接PM交AB于点E,连接PN交AC于点F,过点M作MD⊥PN于点D,设BP=x(0≤x≤4),则PE= ![]() x,CP=4﹣x,PF=
x,CP=4﹣x,PF= ![]() (4﹣x),根据等边三角形的性质结合轴对称的性质即可得出PM、PN的长度,由角的计算可得出∠MPD=60°,进而可得出MD、PD的长度,在Rt△MDN中,利用勾股定理即可得出MN2=MD2+ND2=3(x﹣2)2+36,再根据二次函数的性质即可解决最值问题.
(4﹣x),根据等边三角形的性质结合轴对称的性质即可得出PM、PN的长度,由角的计算可得出∠MPD=60°,进而可得出MD、PD的长度,在Rt△MDN中,利用勾股定理即可得出MN2=MD2+ND2=3(x﹣2)2+36,再根据二次函数的性质即可解决最值问题.
(方法三)连接AM、AN、AP,过点A作AD⊥MN于点D,由对称性可知AM=AP=AN、△MAN为顶角为120°的等腰三角形,进而即可得出MN= ![]() AP,再根据AP的取值范围即可得出线段MN长的取值范围.
AP,再根据AP的取值范围即可得出线段MN长的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校改造一个边长为
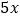 米的正方形花坛,经规划后,南北向要缩短
米的正方形花坛,经规划后,南北向要缩短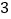 米,东西向要加长
米,东西向要加长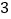 米,则改造后花坛的面积是________平方米,改造后花坛的面积减少了________平方米.
米,则改造后花坛的面积是________平方米,改造后花坛的面积减少了________平方米. -
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.
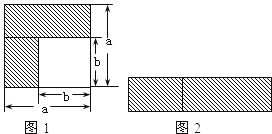
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.例如:
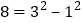 ,
,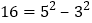 ,
,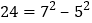 ;则
;则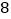 、
、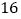 、
、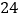 这三个数都是奇特数.
这三个数都是奇特数. (1)
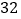 和
和 这两个数是奇特数吗?若是,表示成两个连续奇数的平方差形式.
这两个数是奇特数吗?若是,表示成两个连续奇数的平方差形式.(2)设两个连续奇数是
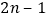 和
和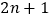 (其中
(其中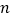 取正整数),由这两个连续奇数构造的奇特数是
取正整数),由这两个连续奇数构造的奇特数是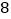 的倍数吗?为什么?
的倍数吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】小慧根据学习函数的经验,对函数y=|x﹣1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x﹣1|的自变量x的取值范围是 ;
(2)列表,找出y与x的几组对应值.
x
…
﹣1
0
1
2
3
…
y
…
b
1
0
1
2
…
其中,b= ;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
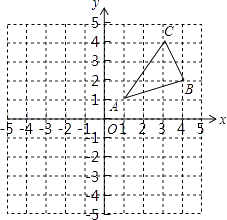
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.

(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
相关试题

