【题目】如图,在△ABC中.AC=BC=5.AB=6.CD是AB边中线.点P从点C出发,以每秒2.5个单位长度的速度沿C-D-C运动.在点P出发的同时,点Q也从点C出发,以每秒2个单位长度的速度沿边CA向点A运动.当一个点停止运动时,另一个点也随之停止,设点P运动的时间为t秒.
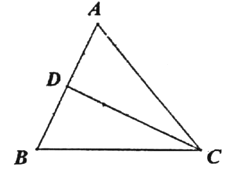
(1)用含t的代数式表示CP、CQ的长度.
(2)用含t的代数式表示△CPQ的面积.
(3)当△CPQ与△CAD相似时,直接写出t的取值范围.
参考答案:
【答案】(1)当0<t≤![]() 时,CP=2.5t,CQ=2t;当
时,CP=2.5t,CQ=2t;当![]() 时,CP=8-2.5t,CQ=2t.
时,CP=8-2.5t,CQ=2t.
(2)当0<t≤![]() 时,S△CPQ=
时,S△CPQ=![]() PCsin∠ACDCQ=
PCsin∠ACDCQ=![]() ×2.5t×
×2.5t×![]() ×2t=
×2t=![]() ;当
;当![]() 时,S△CPQ=
时,S△CPQ=![]() PCsin∠ACDCQ=
PCsin∠ACDCQ=![]() ×(8-2.5t)×
×(8-2.5t)×![]() ×2t=
×2t=![]() .
.
(3)0<t≤![]() 或
或![]() s
s
【解析】
(1)分两种情形:当0<t≤![]() 时,当
时,当![]() <t
<t![]() 时,分别求解即可.
时,分别求解即可.
(2)分两种情形:当0<t≤![]() 时,当
时,当![]() <t≤
<t≤![]() 时,根据S△CPQ=
时,根据S△CPQ=![]() PCsin∠ACDCQ分别求解即可.
PCsin∠ACDCQ分别求解即可.
(3)分两种情形:当0<t≤![]() ,可以证明△QCP∽△DCA,当
,可以证明△QCP∽△DCA,当![]() <t
<t![]() ,∠QPC=90°时,△QPC∽△ADC,构建方程求解即可.
,∠QPC=90°时,△QPC∽△ADC,构建方程求解即可.
解:(1)∵CA=CB,AD=BD=3,
∴CD⊥AB,
∴∠ADC=90°,
∴CD=![]() =
=![]() =4,
=4,
当0<t≤![]() 时,CP=2.5t,CQ=2t,
时,CP=2.5t,CQ=2t,
当![]() 时,CP=8-2.5t,CQ=2t.
时,CP=8-2.5t,CQ=2t.
(2)∵sin∠ACD=![]() =
=![]() ,
,
∴当0<t≤![]() 时,S△CPQ=
时,S△CPQ=![]() PCsin∠ACDCQ=
PCsin∠ACDCQ=![]() ×2.5t×
×2.5t×![]() ×2t=
×2t=![]()
当![]() 时,S△CPQ=
时,S△CPQ=![]() PCsin∠ACDCQ=
PCsin∠ACDCQ=![]() ×(8-2.5t)×
×(8-2.5t)×![]() ×2t=
×2t=![]() .
.
(3)①当0<t≤![]() 时,
时,
∵CP=2.5t,CQ=2t,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴![]() ,
,
∵∠PCQ=∠ACD,
∴0<t≤![]() 时,△QCP∽△DCA,
时,△QCP∽△DCA,
②当![]() 时,当∠QPC=90°时,△QPC∽△ADC,
时,当∠QPC=90°时,△QPC∽△ADC,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
综上所述,满足条件的t的值为:0<t≤![]() 或
或![]() s时,△QCP∽△DCA.
s时,△QCP∽△DCA.
-
科目: 来源: 题型:
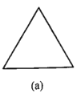
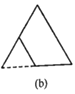
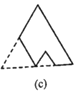
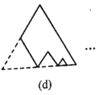
查看答案和解析>>【题目】如图所示,图(a)是一块边长为1,周长记为
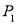 的正三角形纸板,沿图(a)的底边剪去一块边长为
的正三角形纸板,沿图(a)的底边剪去一块边长为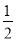 的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的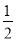 后,得图(c),(d),……,记第
后,得图(c),(d),……,记第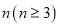 )块纸板的周长为Pn.则
)块纸板的周长为Pn.则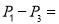 ____;
____;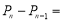 _______.
_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于给定的一次函数y=ax+b(a≠0),把形如
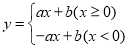 的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).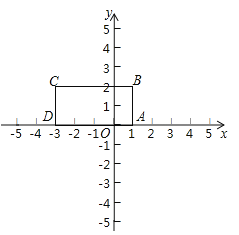
(1)已知函数y=2x+l.
①若点P(-1,m)在这个一次函数的衍生函数图像上,则m= .
②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .
(2)当函数y=kx-3(k>0)的衍生函数的图象与矩形ABCD有2个交点时,k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(
 ,
, )
)B. 当m>0时,函数图象截x轴所得的线段长度大于

C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>
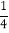 时,y随x的增大而减小
时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:
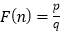 、例如18可以分解成1×18,2×9,3×6这三种,这时就有
、例如18可以分解成1×18,2×9,3×6这三种,这时就有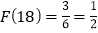 .给出下列关于F(n)的说法:(1)
.给出下列关于F(n)的说法:(1)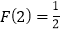 ;(2)
;(2)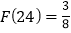 ;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____. -
科目: 来源: 题型:
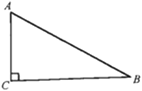
查看答案和解析>>【题目】如图所示,在
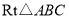 中,
中,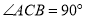 ,
,(1)用尺规在边BC上求作一点P,使
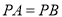 ;(不写作法,保留作图痕迹)
;(不写作法,保留作图痕迹)(2)连接AP当
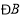 为多少度时,AP平分
为多少度时,AP平分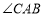 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1、x2,则(x1﹣1)2+(x2﹣1)2的最小值是_____.
相关试题

