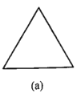
【题目】如图所示,图(a)是一块边长为1,周长记为![]() 的正三角形纸板,沿图(a)的底边剪去一块边长为
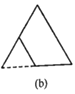
的正三角形纸板,沿图(a)的底边剪去一块边长为![]() 的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
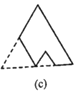
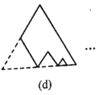
的正三角形纸板后得到图(b),然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的![]() 后,得图(c),(d),……,记第
后,得图(c),(d),……,记第![]() )块纸板的周长为Pn.则
)块纸板的周长为Pn.则![]() ____;
____;![]() _______.
_______.
参考答案:
【答案】![]()
![]()
【解析】
根据等边三角形的性质(三边相等)求出等边三角形的周长P1,P2,P3,P4,……根据周长相减的结果能找到规律即可求出答案.
P1=1+1+1=3,
P2=1+1+![]() =
=![]() ,
,
P3=1+1+![]() ×3=
×3=![]() ,
,
P4=1+1+![]() ×2+
×2+![]() ×3=
×3=![]() ,
,
…
∴P1-P3=3-![]() =
=![]() ,
,
p3-p2=![]() -
-![]() =
=![]() =(
=(![]() )2,
)2,
P4-P3=![]() -
-![]() =
=![]() =(
=(![]() )3,
)3,
∴Pn-Pn-1=![]() =
=![]() ,
,
故答案为:![]() ;
;![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一四柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示,根据图象提供的信息,解答下列问题:
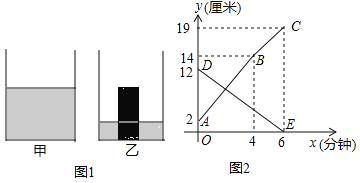
(1)图2中折线ABC表示 槽中水的深度与注水时间关系,线段DE表示 槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点B的纵坐标表示的实际意义是 .
(2)注水多长时间时,甲、乙.两个水槽中水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),则乙槽中铁块的体积为 立方厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图l,在四边形ABCD中.∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”∠DAB称为“可分角”.

(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,求证:△DAC∽△CAB.
(2)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB 则∠DAB = .
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4.BC=2.∠D=90°,则AD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有
 、
、 、
、 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )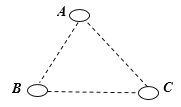
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于给定的一次函数y=ax+b(a≠0),把形如
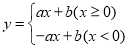 的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).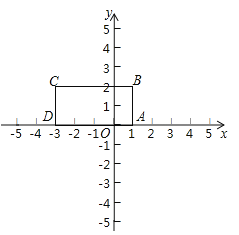
(1)已知函数y=2x+l.
①若点P(-1,m)在这个一次函数的衍生函数图像上,则m= .
②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .
(2)当函数y=kx-3(k>0)的衍生函数的图象与矩形ABCD有2个交点时,k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(
 ,
, )
)B. 当m>0时,函数图象截x轴所得的线段长度大于

C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>
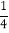 时,y随x的增大而减小
时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中.AC=BC=5.AB=6.CD是AB边中线.点P从点C出发,以每秒2.5个单位长度的速度沿C-D-C运动.在点P出发的同时,点Q也从点C出发,以每秒2个单位长度的速度沿边CA向点A运动.当一个点停止运动时,另一个点也随之停止,设点P运动的时间为t秒.
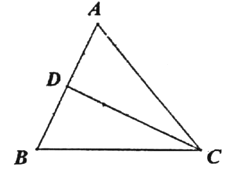
(1)用含t的代数式表示CP、CQ的长度.
(2)用含t的代数式表示△CPQ的面积.
(3)当△CPQ与△CAD相似时,直接写出t的取值范围.
相关试题

