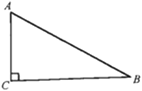
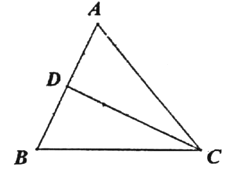
【题目】如图所示,在![]() 中,
中,![]() ,
,
(1)用尺规在边BC上求作一点P,使![]() ;(不写作法,保留作图痕迹)
;(不写作法,保留作图痕迹)
(2)连接AP当![]() 为多少度时,AP平分
为多少度时,AP平分![]() .
.
参考答案:
【答案】(1)详见解析;(2)30°.
【解析】
(1)根据线段垂直平分线的作法作出AB的垂直平分线即可;
(2)连接PA,根据等腰三角形的性质可得![]() ,由角平分线的定义可得
,由角平分线的定义可得![]() ,根据直角三角形两锐角互余的性质即可得∠B的度数,可得答案.
,根据直角三角形两锐角互余的性质即可得∠B的度数,可得答案.
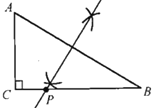
(1)如图所示:分别以A、B为圆心,大于![]() AB长为半径画弧,两弧相交于点E、F,作直线EF,交BC于点P,
AB长为半径画弧,两弧相交于点E、F,作直线EF,交BC于点P,
∵EF为AB的垂直平分线,
∴PA=PB,
∴点P即为所求.
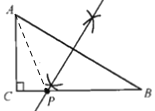
(2)如图,连接AP,
∵![]() ,
,
∴![]() ,
,
∵AP是角平分线,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴∠PAC+∠PAB+∠B=90°,
∴3∠B=90°,
解得:∠B=30°,
∴当![]() 时,AP平分
时,AP平分![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(
 ,
, )
)B. 当m>0时,函数图象截x轴所得的线段长度大于

C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>
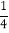 时,y随x的增大而减小
时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中.AC=BC=5.AB=6.CD是AB边中线.点P从点C出发,以每秒2.5个单位长度的速度沿C-D-C运动.在点P出发的同时,点Q也从点C出发,以每秒2个单位长度的速度沿边CA向点A运动.当一个点停止运动时,另一个点也随之停止,设点P运动的时间为t秒.
(1)用含t的代数式表示CP、CQ的长度.
(2)用含t的代数式表示△CPQ的面积.
(3)当△CPQ与△CAD相似时,直接写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:
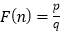 、例如18可以分解成1×18,2×9,3×6这三种,这时就有
、例如18可以分解成1×18,2×9,3×6这三种,这时就有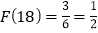 .给出下列关于F(n)的说法:(1)
.给出下列关于F(n)的说法:(1)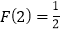 ;(2)
;(2)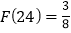 ;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1、x2,则(x1﹣1)2+(x2﹣1)2的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.
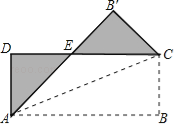
(1)求证:△AED≌△CEB′;
(2)求证:点E在线段AC的垂直平分线上;
(3)若AB=8,AD=3,求图中阴影部分的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于另一点Q,如果QP=QO,则∠OCP= .

相关试题

