【题目】点C、D在线段AB上,若点C是线段AD的中点,2BD>AD,则下列结论正确的是( ).
A. CD<AD- BD B. AB>2BD C. BD>AD D. BC>AD
参考答案:
【答案】D
【解析】
根据点C是线段AD的中点,可得AD=2AC=2CD,再根据2BD>AD,可得BD> AC= CD,
再根据线段的和差,逐一进行判即可。
∵点C是线段AD的中点,
∴AD=2AC=2CD,
∵2BD>AD,
∴BD> AC= CD,
A. CD=AD-AC> AD- BD,该选项错误;
B. 由A得AD- BD![]() CD,则AD
CD,则AD![]() BD+CD=BC,则AB=AD+BD
BD+CD=BC,则AB=AD+BD![]() BC+ BD
BC+ BD![]() 2BD,该选项错误;
2BD,该选项错误;
C.由B得 AB![]() 2BD ,则BD+AD
2BD ,则BD+AD![]() 2BD,则AD
2BD,则AD![]() BD,该选项错误;
BD,该选项错误;
D. 由A得AD- BD![]() CD,则AD
CD,则AD![]() BD+CD=BC, 该选项正确
BD+CD=BC, 该选项正确
故选:D.
-
科目: 来源: 题型:
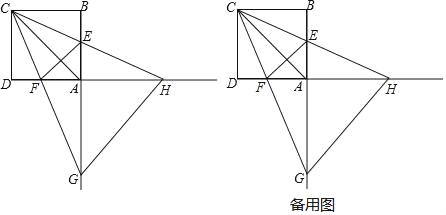
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(2,0),B(1,-1),将线段OA绕点O逆时针旋转,旋转角为
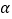 (0°<
(0°<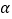 <135°).记点A的对应点为A1,若点A1与点B的距离为
<135°).记点A的对应点为A1,若点A1与点B的距离为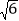 ,则
,则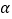 为( ).
为( ).A. 30° B. 45° C. 60° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把三边长的比为3:4:5的三角形称为完全三角形,记命题A:“完全三角形是直角三角形”.若命题B是命题A的逆命题,请写出命题B:______________________;并写出一个例子(该例子能判断命题B是错误的)
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:
如图1,
 中,
中, ,
, 于点
于点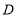 ,
, 且
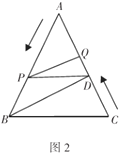
且 ;如图2,在图1的基础上,动点
;如图2,在图1的基础上,动点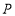 从点
从点 出发以每秒
出发以每秒 的速度沿线段
的速度沿线段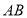 向点
向点 运动,同时动点
运动,同时动点 从点
从点 出发以相同速度沿线段
出发以相同速度沿线段 向点
向点 运动,当其中一点到达终点时另外一点也随之停止运动,设点
运动,当其中一点到达终点时另外一点也随之停止运动,设点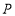 运动的时间为
运动的时间为 秒.
秒.(1)求
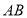 的长;
的长;(2)当
 的其中一边与
的其中一边与 平行时(
平行时( 与
与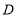 不重合),求
不重合),求 的值;
的值;(3)点
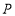 在线段
在线段 上运动的过程中,是否存在以
上运动的过程中,是否存在以 为腰的
为腰的 是等腰三角形?若存在,求出
是等腰三角形?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的弦,P为AB的中点,连接OA、OP,将△OPA绕点O旋转到△OQB.设⊙O的半径为1,∠AOQ=135°,则AQ的长为______
相关试题

