【题目】综合与实践:
如图1,![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 且
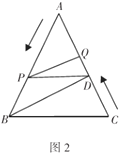
且![]() ;如图2,在图1的基础上,动点
;如图2,在图1的基础上,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度沿线段
的速度沿线段![]() 向点
向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发以相同速度沿线段
出发以相同速度沿线段![]() 向点
向点![]() 运动,当其中一点到达终点时另外一点也随之停止运动,设点
运动,当其中一点到达终点时另外一点也随之停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 的长;
的长;
(2)当![]() 的其中一边与
的其中一边与![]() 平行时(
平行时(![]() 与
与![]() 不重合),求
不重合),求![]() 的值;
的值;
(3)点![]() 在线段
在线段![]() 上运动的过程中,是否存在以
上运动的过程中,是否存在以![]() 为腰的
为腰的![]() 是等腰三角形?若存在,求出
是等腰三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.


参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 的值为2.5秒或3秒;(3)存在,
的值为2.5秒或3秒;(3)存在,![]() 的值为3或
的值为3或![]() 秒.
秒.
【解析】
(1)设![]() ,
,![]() ,则
,则![]() ,在Rt△ABD中利用勾股定理建立方程求出x,即可得到AB的长;
,在Rt△ABD中利用勾股定理建立方程求出x,即可得到AB的长;
(2)分两种情况讨论:①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ,分别建立方程求解;
,分别建立方程求解;
(3)分两种情况讨论:①当![]() 时,易得
时,易得![]() ;②当
;②当![]() 时,过点
时,过点![]() 作
作![]() 于点
于点![]() ,利用等积法求出DE,再用勾股定理求出AE,进而得到AP,用距离除以速度即可得出时间.
,利用等积法求出DE,再用勾股定理求出AE,进而得到AP,用距离除以速度即可得出时间.
解:(1)设![]() ,
,![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ,
,
∴![]() .
.
(2)由(1)可得:![]() ,
,![]() ,
,![]() ,
,
∵动点![]() 、
、![]() 以每秒
以每秒![]() 的速度运动,时间为
的速度运动,时间为![]() ,
,
∴![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,
即![]() ,
,
∴![]() ;
;
②当![]() 时,
时,![]() ,
,
即![]() ,
,
∴![]() .
.
∴当![]() 的其中一边与
的其中一边与![]() 平行时,
平行时,![]() 的值为2.5秒或3秒.
的值为2.5秒或3秒.
(3)存在,分两种情况讨论:
①如图,当![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
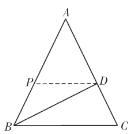
∴![]() ,
,
∴![]() ,
,
②如图,当![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
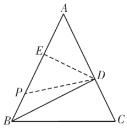
过点![]() 作
作![]() 于点
于点![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,
,
∴![]() ,
,
在![]() 中,
中,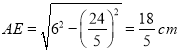 .
.
∴![]() ,
,
∴![]() .
.
综上,当![]() 的值为3或
的值为3或![]() 秒时,
秒时,![]() 是以
是以![]() 为腰的等腰三角形.
为腰的等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知A(2,0),B(1,-1),将线段OA绕点O逆时针旋转,旋转角为
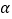 (0°<
(0°<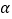 <135°).记点A的对应点为A1,若点A1与点B的距离为
<135°).记点A的对应点为A1,若点A1与点B的距离为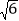 ,则
,则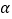 为( ).
为( ).A. 30° B. 45° C. 60° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】点C、D在线段AB上,若点C是线段AD的中点,2BD>AD,则下列结论正确的是( ).
A. CD<AD- BD B. AB>2BD C. BD>AD D. BC>AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把三边长的比为3:4:5的三角形称为完全三角形,记命题A:“完全三角形是直角三角形”.若命题B是命题A的逆命题,请写出命题B:______________________;并写出一个例子(该例子能判断命题B是错误的)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的弦,P为AB的中点,连接OA、OP,将△OPA绕点O旋转到△OQB.设⊙O的半径为1,∠AOQ=135°,则AQ的长为______
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线y=x2+bx(b>2)上存在关于直线y=x成轴对称的两个点,则b的取值范围是______.
-
科目: 来源: 题型:
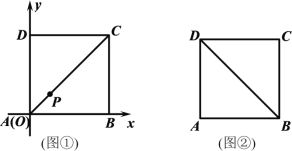
查看答案和解析>>【题目】已知动点P在边长为1的正方形ABCD的内部,点P到边AD、AB的距离分别为m、n.
(1)以A为原点,以边AB所在直线为x轴,建立平面直角坐标系,如图①所示,当点P在对角线AC上,且m=
 时,求点P的坐标;
时,求点P的坐标;(2)如图②,当m、n满足什么条件时,点P在△DAB的内部?请说明理由.
相关试题

