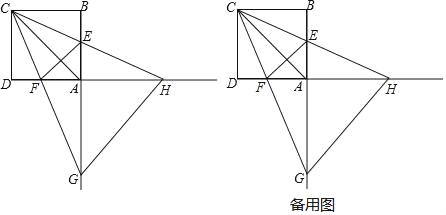
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
参考答案:
【答案】(1)=;(2)结论:AC2=AGAH.理由见解析;(3)①△AGH的面积不变.②m的值为![]() 或3或12﹣6
或3或12﹣6![]() ..
..
【解析】
(1)证明∠DAC=∠AHC+∠ACH=45°,∠ACH+∠ACG=45°,即可推出∠AHC=∠ACG;
(2)结论:AC2=AGAH.只要证明△AHC∽△ACG即可解决问题;
(3)①△AGH的面积不变.理由三角形的面积公式计算即可;
②分三种情形分别求解即可解决问题.
(1)∵四边形ABCD是正方形,
∴AB=CB=CD=DA=4,∠D=∠DAB=90°∠DAC=∠BAC=45°,
∴AC=![]() ,
,
∵∠DAC=∠AHC+∠ACH=45°,∠ACH+∠ACG=45°,
∴∠AHC=∠ACG.
故答案为=.
(2)结论:AC2=AGAH.
理由:∵∠AHC=∠ACG,∠CAH=∠CAG=135°,
∴△AHC∽△ACG,
∴![]() ,
,
∴AC2=AGAH.
(3)①△AGH的面积不变.
理由:∵S△AGH=![]() AHAG=
AHAG=![]() AC2=
AC2=![]() ×(4
×(4![]() )2=16.
)2=16.
∴△AGH的面积为16.
②如图1中,当GC=GH时,易证△AHG≌△BGC,
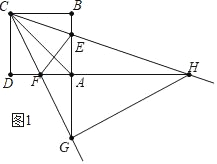
可得AG=BC=4,AH=BG=8,
∵BC∥AH,
∴![]() ,
,
∴AE=![]() AB=
AB=![]() .
.
如图2中,当CH=HG时,
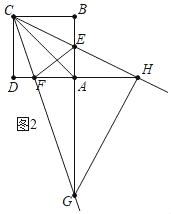
易证AH=BC=4,
∵BC∥AH,
∴![]() =1,
=1,
∴AE=BE=3.
如图3中,当CG=CH时,易证∠ECB=∠DCF=22.5.
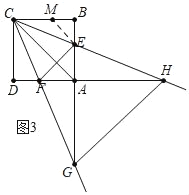
在BC上取一点M,使得BM=BE,
∴∠BME=∠BEM=45°,
∵∠BME=∠MCE+∠MEC,
∴∠MCE=∠MEC=22.5°,
∴CM=EM,设BM=BE=m,则CM=EM![]() m,
m,
∴m+![]() m=6,
m=6,
∴m=6(![]() ﹣1),
﹣1),
∴AE=6﹣6(![]() ﹣1)=12﹣6
﹣1)=12﹣6![]() ,
,
综上所述,满足条件的m的值为![]() 或3或12﹣6
或3或12﹣6![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的方格纸中,每一个小正方形的边长都为1.
(1)∠BCD是不是直角?请说明理由;
(2)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△
 中,
中,  .取
.取 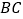 边的中点
边的中点 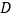 ,作
,作  ⊥
⊥  于点
于点  ,取
,取  的中点
的中点 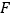 ,连接
,连接  ,
,  交于点
交于点  .
.
(1)如图1,如果 ,求证:
,求证:  ⊥
⊥  并求
并求  的值;
的值;
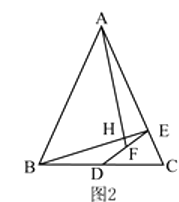
(2)如图2,如果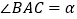 ,求证:
,求证:  ⊥
⊥  并用含
并用含  的式子表示
的式子表示  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答会告诉你方法.
(1)阅读下列材料:
问题:利用一元一次方程将
 化成分数.
化成分数.解:设
 .
.方程两边都乘以10,可得
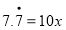 .
.由
 和
和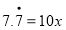 ,可得
,可得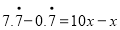 即
即 .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)解得
 ,即
,即 .
.填空:将0.
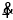 写成分数形式为 .
写成分数形式为 .(2)请你仿照上述方法把小数1.
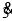 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 的图像交
的图像交  轴于
轴于 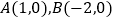 ,交
,交  轴于点
轴于点  ,连接直线
,连接直线  .
.
(1)求二次函数的解析式;
(2)点 在二次函数的图像上,圆
在二次函数的图像上,圆  与直线
与直线  相切,切点为
相切,切点为  .
.
①若 在
在  轴的左侧,且△
轴的左侧,且△  ∽△
∽△  ,求点
,求点  的坐标;
的坐标;
②若圆 的半径为4,求点
的半径为4,求点  的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A.
 B.
B.  C. 3 D.
C. 3 D. 
相关试题

